费尔马点定理(费马尔点是什么)

导语：费尔马点性质的证明

1640年，费尔马提出如下著名的几何问题：A、B、C任意三点，在平面上确定一点F，使FA＋FB＋FC最小，点F称为费尔马点。

费尔马点有三种情况：

1、当B、A、C三点不共线，△ABC三内角都小于120°时，费尔马点F在△ABC内部，且∠AFB＝∠BFC＝∠CFA＝120° 。

2、当B 、A、C三点不共线，△ABC有某内角≥120°时，费尔马点是最大内角的顶点；

3、B、A、C三点共线时，∠BAC＝180°，A为费尔马点。

证明：1、当费尔马点F在△ABC内部时，不是随便可以确定费尔马点F的，我们必须先作F点。

如图分别以AB、AC向△ABC外作正△ACD和正△ABE，连接BD、EC交于F点，则F点为费尔马点。理由如下：连AF，可证△ABD≌△ACE（SAS），得∠1＝∠2，A、E、B、F四点共圆（还有其它方法可证明），∵∠AEB＝60°，∴∠AFB＝120°（圆内接四边形对角互补）同理：∠CFA＝120°，∵A、E、B、F四点共圆，∠3＝∠4＝60°，∴∠BFC＝120°。

即∠AFB＝∠BFC＝∠CFA，∴F点为费尔马点。再证FA＋FB＋FC最小

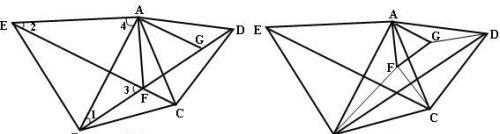
将△AFC绕A点逆时针旋转60°得△AGD，如图1

则FC＝GD，且△AFG是正三角形，∴FA＝FG，∴FA＋FB＋FC＝FG＋FB＋GD＝BD（最小值）。

当F点在其它位置时，如图2，将△AFC绕A点逆时针旋转60º得△AGD，可证FA＋FB＋FC＝FB＋FG＋GD＞BD

2、：当△ABC有某内角≥120°时，费尔马点是最大内角的顶点；

证明：不妨设∠A≥120°，如图3，下面我们来证A是费尔马点，即证：F是平面上任意一点，FA＋FB＋FC＞AB＋AC

将△FAB绕A点顺时针旋转，使B点落在CA的延长线上的B′处，如图(F点在各种位置)。连FB′

∵∠BAC≥60°,∴则旋转角α≤60°,在△AFF′中，AF＝AF′，α≤60°，

∴∠ AF′F≥60°，∴FA≥F F′，∵FB＝F′B′

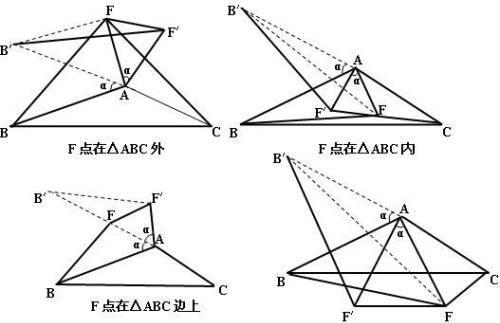
∴FA＋FB＋FC＝FA＋F′B′＋FC≥(FF′＋F′B′)＋FC＞FB′＋FC＞B′C

∵B′C＝AB′＋AC，而AB′＝AB，∴B′C＝AB＋AC

∴FA＋FB＋FC＞AB＋AC，∴A为费尔马点。

当BAC共线时，∠BAC＝180°，A为费尔马点也成立。

综上所述，费尔马点性质得证。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小薇创作整理编辑！