初二数学几何是关键一定要重视吗(初二数学几何是关键一定要重视数学吗)

导语：初二数学几何是关键，一定要重视

几何模型3—一线三等角模型

【模型介绍】

一线三等角：两个三角形中相等的两个角落在同一条直线上，另外两条边所构成的角与这两个角相等，这三个相等的角落在同一直线上，故称“一线三等角”

如下图所示，一线三等角包括一线三直角、一线三锐角、一线三钝角

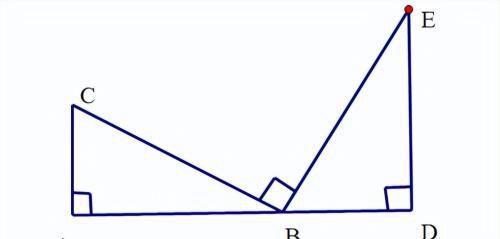
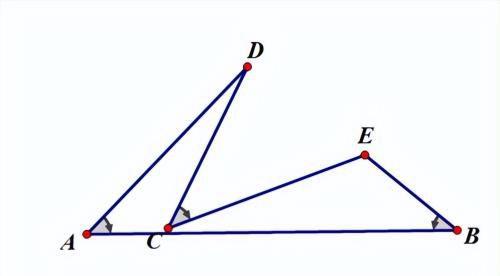
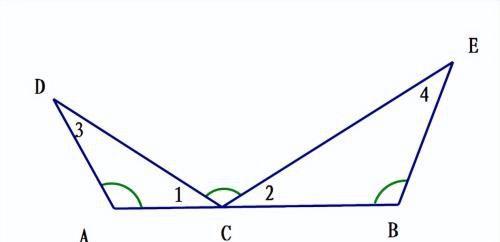
【解题关键】

构造相似或是全等三角形

【典型例题】

【题型一：一线三直角模型】

如图，若∠1、∠2、∠3都为直角，则有△ACP∽△BPD．

【例1】如图1所示，已知中，，直线m经过点C，过A、B两点分别作直线m的垂线，垂足分别为E、F．

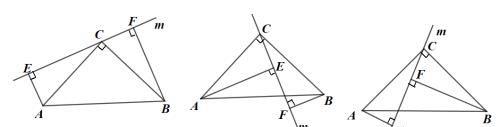
（1）如图1，当直线m在A、B两点同侧时，求证：；

（2）若直线m绕点C旋转到图2所示的位置时（），其余条件不变，猜想与，有什么数量关系？并证明你的猜想；

（3）若直线m绕点C旋转到图3所示的位置时（）其余条件不变，问与，的关系如何？直接写出猜想结论，不需证明．

【答案】（1）见解析；

（2），证明见解析；

（3），证明见解析

【解析】

（1）证明：，，，

∴∠AEC=∠BFC=∠ACB=90°，

∴∠EAC+∠ECA=90°，∠FCB+∠ECA=90°，

∴∠EAC=∠FCB，

在和中，

，

，

，，

∵，

∴；

（2）解：，理由如下：

，，，

∴∠AEC=∠BFC=∠ACB=90°，

∴∠EAC+∠ECA=90°，∠FCB+∠ECA=90°，

∴∠EAC=∠FCB，

在和中，

，

，

，，

∵，

∴；

（3）解：，理由如下：

，，，

∴∠AEC=∠BFC=∠ACB=90°，

∴∠EAC+∠ECA=90°，∠FCB+∠ECA=90°，

∴∠EAC=∠FCB，

在和中，

，

，

，，

∵，

∴．

【练1】如图，在平面直角坐标系中，将直线向上平移3个单位，与轴、轴分别交于点A、B，以线段AB为斜边在第一象限内作等腰直角三角形ABC．若反比例函数的图象经过点C，则的值为（ ）

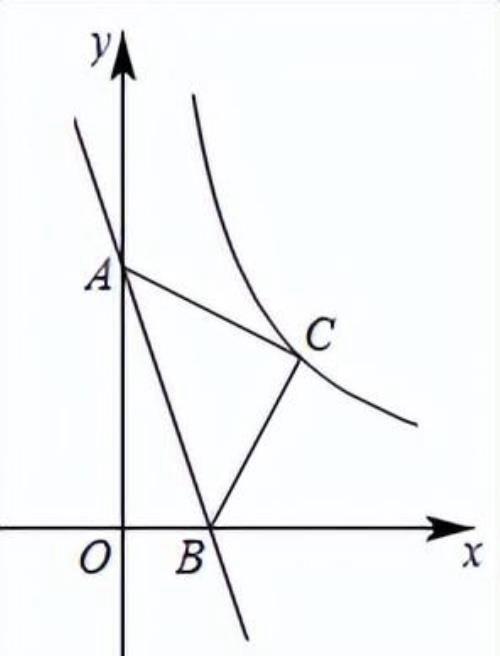
A．2 B．3 C．4 D．6

【答案】C

【解析】解：过点C作CE⊥x轴于点E，作CF⊥y轴于点F，如图所示，

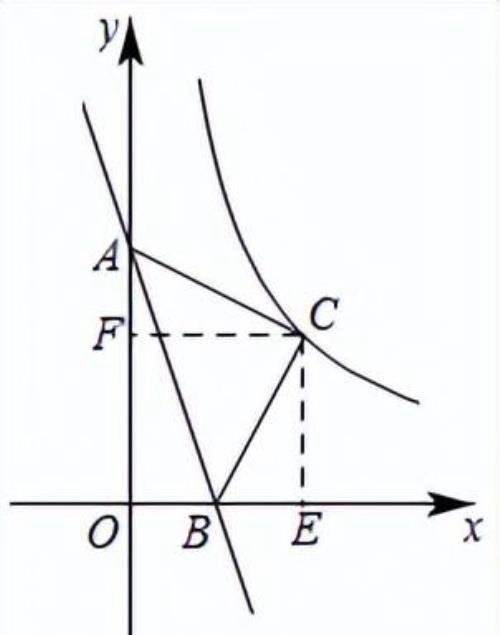
∵CE⊥x轴，CF⊥y轴，

∴∠ECF＝90°．

∵△ABC为等腰直角三角形，

∴∠ACF＋∠FCB＝∠FCB＋∠BCE＝90°，AC＝BC，

∴∠ACF＝∠BCE．

在△ACF和△BCE中，

，

∴△ACF≌△BCE（AAS），

∴S△ACF＝S△BCE，

∴S矩形OECF＝S四边形OBCA＝S△AOB＋S△ABC．

∵将直线y＝−3x向上平移3个单位可得出直线AB，

∴直线AB的表达式为y＝−3x＋3，

∴点A（0，3），点B（1，0），

∴，

∵△ABC为等腰直角三角形，

∴，

∴S矩形OECF＝S△AOB＋S△ABC＝×1×3＋＝4．

∵反比例函数（x＞0）的图象经过点C，

∴k＝4，

故选C．

【练2】如图，直角三角形的直角顶点在坐标原点，，若点A在反比例函数的图象上，则经过点B的反比例函数表达式为（ ）

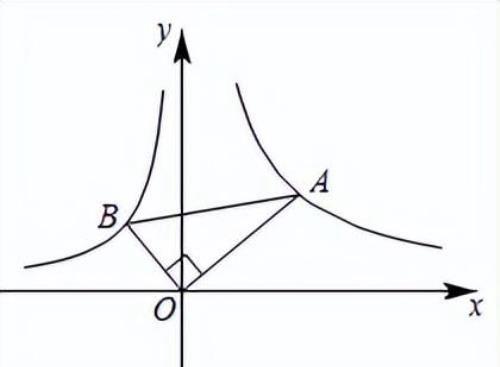
A． B． C．

D．

【答案】C

【解析】解：作轴于D，轴于C，如图，

∵，，

∴，

∴．

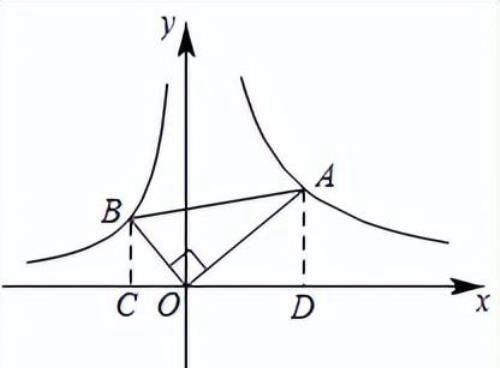
∵点A在反比例函数的图象上，

∴．

∵，，

∴，

∴Rt△BOC∽Rt△OAD，

∴．

∵，

∴，

即，

∴．

∵，

∴，

∴经过点B的反比例函数解析式为．

故选：C．

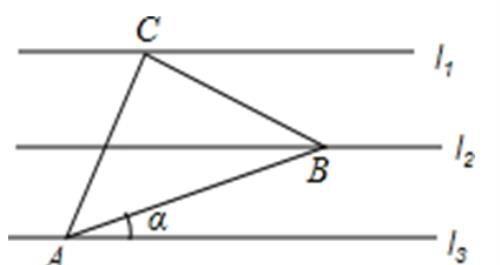
【练3】如图，已知，相邻两条平行直线间的距离相等，若等腰直角△ABC的三个顶点分别在这三条平行直线上，则的值是（ ）

A． B. C． D.

【答案】D

【解析】如图，过点A作AD⊥于点D，过点B作BE⊥于点B，设，，之间的距离为1

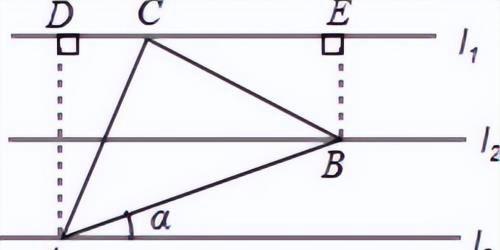
∵∠CAD+∠ACD=90°，∠BCE+∠ACD=90°

∴∠CAD=∠BCE

在等腰直角△ABC中，AC=BC，∠ADC=∠BEC=90°

∴△ACD≌△CBE

∴CD=BE=1

在Rt△ACD中

AC=

在等腰直角△ABC中

AB=AC=

∴

故选：D

【练4】如图1，等腰Rt△ABC中，∠ABC＝90°，CB＝BA，直线ED经过点B，过A作AD⊥ED于D，过C作CE⊥ED于E.则易证△ADB≌△BEC．这个模型我们称之为“一线三垂直”.它可以把倾斜的线段AB和直角∠ABC转化为横平竖直的线段和直角，所以在平面直角坐标系中被大量使用.

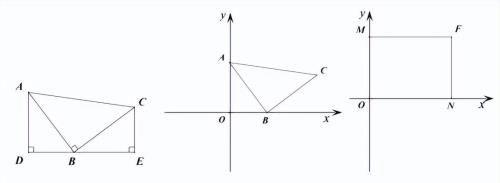
模型应用：

(1)如图2，点A（0，4)，点B(3，0），△ABC是等腰直角三角形．

①若∠ABC＝90°，且点C在第一象限，求点C的坐标；

②若AB为直角边，求点C的坐标；

(2)如图3，长方形MFNO，O为坐标原点，F的坐标为（8，6），M、N分别在坐标轴上，P是线段NF上动点，设PN＝n，已知点G在第一象限，且是直线y＝2x一6上的一点，若△MPG是以G为直角顶点的等腰直角三角形，请直接写出点G的坐标.

【答案】（1）①（7,3）；②（7,3）、（4,7）、（-4,1）、（-1,-3）；

（2）（4，2）、.

【解析】解：（1）①如图，过C作CD垂直于x轴，

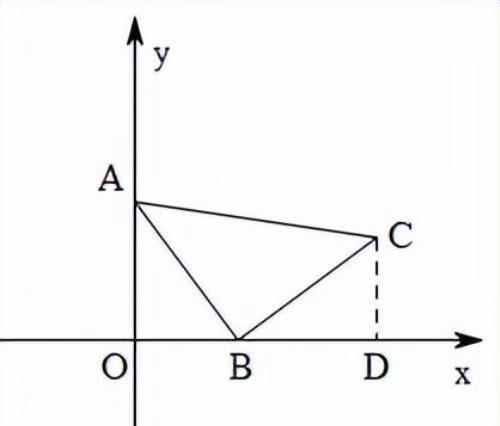
根据“一线三垂直”可得△AOB≌△BDC，∴AO=BD，OB=CD，

∵点A（0，4)，点B(3，0），∴AO=4，OB=3 ，

∴OD=3+4=7，

∴点C的坐标为（7,3）；

②如图，若AB为直角边，点C的位置可有4处，

a、若点C在①的位置处，则点C的坐标为（7,3）；

b、若点C在的位置处，同理可得，则点的坐标为（4,7）；

c、若点C在的位置处，则、关于点A对称，

∵点A（0，4)，点（4,7），∴点的坐标为（-4,1）；

d、若点C在的位置处，则、C关于点B对称，

∵点B(3，0），点C（7,3），∴点的坐标为（-1,-3）；

综上，点C的坐标为（7,3）、（4,7）、（-4,1）、（-1,-3）；

（2）当点G位于直线y=2x-6上时，分两种情况：

①当点G在矩形MFNO的内部时，如图，过G作x轴的平行线AB，交y轴于A，交直线NF于点B，设G（x，2x-6）；

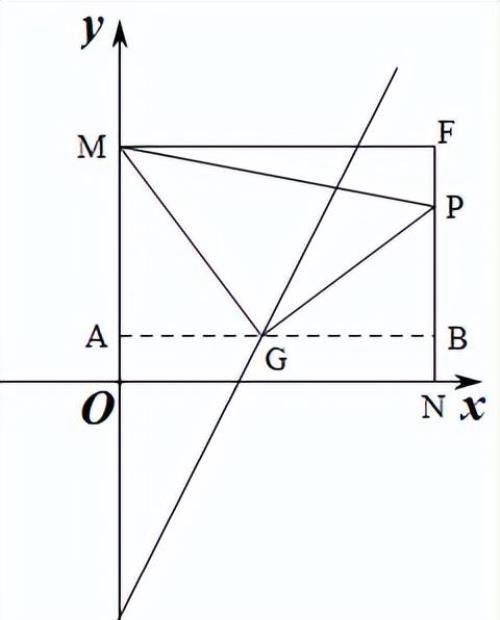
则OA=2x-6，AM=6-（2x-6）=12-2x，BG=AB-AG=8-x；

则△MAG≌△GBP，得AM =BG，

即：12-2x=8-x，解得x=4，

∴G（4，2）；

当点G在矩形MFNO的外部时，如图，过G作x轴的平行线AB，交y轴于A，交直线NF的延长线于点B，设G（x，2x-6）；

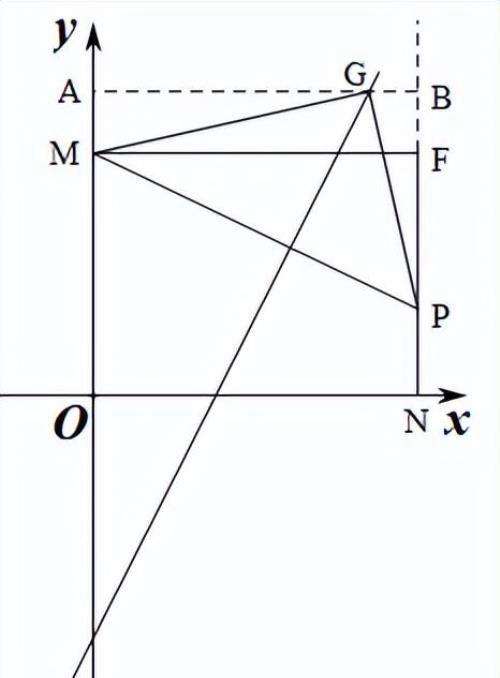
则OA=2x-6，AM=（2x-6）-6=2x-12，BG=AB-AG=8-x；

则△MAG≌△GBP，得AM =BG，

即：2x-12=8-x，解得，

∴G ；

综上，G点的坐标为（4，2）、.

【题型二：一线三锐角与一线三钝角】

如图，若∠1、∠2、∠3都为锐角，则有△ACP∽△BPD．

证明：∵∠DPB＝180°－∠3－∠CPA，∠C＝180°－∠1－∠CPA，而∠1＝∠3

∴∠C＝∠DPB，

∵∠1＝∠2，

∴△ACP∽△BPD

如图，若∠1、∠2、∠3都为钝角，则有△ACP∽△BPD．（证明同锐角）

【例2】如图，在等腰三角形ABC中，∠BAC＝120°，AB＝AC＝2，点D是BC边上的一个动点（不与B、C重合），在AC上取一点E，使∠ADE＝30°．

（1）设BD＝x，AE＝y，求y关于x的函数关系式并写出自变量x的取值范围；

（2）当△ADE是等腰三角形时，求AE的长．

【答案】（1）

(2) AE＝4－或AE＝

【解析】解（1）∵△ABC是等腰三角形，且∠BAC＝120°，

∴∠ABD＝∠ACB＝30°，

∴∠ABD＝∠ADE＝30°，

∵∠ADC＝∠ADE＋∠EDC＝∠ABD＋∠DAB，

∴∠EDC＝∠DAB，

∴△ABD∽△DCE；

∵AB＝AC＝2，∠BAC＝120°，

过A作AF⊥BC于F，

∴∠AFB＝90°，

∵AB＝2，∠ABF＝30°，

∴AF＝＝1，

∴BF＝，

∴BC＝2BF＝，

则DC＝，EC＝2－y

∵△ABD∽△DCE，

∴，

∴，

化简得：．

（2）①当AD＝DE时，如图，

△ABD≌△DCE，

则AB＝CD，即2＝，

x＝，代入

解得：y＝，即AE＝，

②当AE＝ED时，如图，

∠EAD＝∠EDA＝30°，∠AED＝120°，

所以∠DEC＝60°，∠EDC ＝90°

则ED＝ EC，即y＝ （2－y）

解得y＝，即AE＝；

③当AD＝AE时，有∠AED－∠EDA＝30°，∠EAD＝120°

此时点D和点B重合，与题目不符，此情况不存在．

所以当△是ADE等腰三角形时，AE＝4－或AE＝

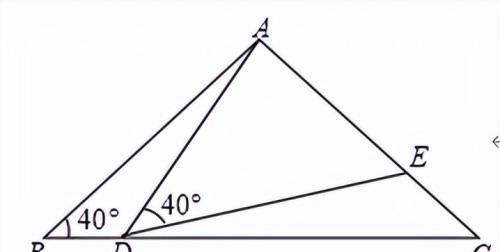
【练1】如图，在△ABC中， AB=AC=2，∠B=40°，点D在线段BC上运动（点D不与点B、C重合），连接AD，作∠ADE=40°，DE交线段AC于点E．

（1）当∠BDA=115°时，∠EDC=______°，∠AED=______°；

（2）线段DC的长度为何值时，△ABD≌△DCE，请说明理由；

（3）在点D的运动过程中，△ADE的形状可以是等腰三角形吗？若可以，求∠BDA的度数；若不可以，请说明理由．

【答案】（1）25°，65°；

（2）2，理由见解析；

（3）可以，110°或80°.

【解析】

解：（1）∵∠B=40°∠ADB=115°，

∴∠BAD=180°-∠B-∠ADB=180°-115°-40°=25°，

∵AB=AC，

∴∠C=∠B=40°，

∵∠EDC=180°-∠ADB-∠ADE=25°，

∴∠DEC=180°-∠EDC-∠C=115°，

∴∠AED=180°-∠DEC=180°-115°=65°；

（2）当DC=2时，△ABD≌△DCE，

理由：∵∠C=40°，

∴∠DEC+∠EDC=140°，

又∵∠ADE=40°，

∴∠ADB+∠EDC=140°，

∴∠ADB=∠DEC，

又∵AB=DC=2，

在△ABD和△DCE中，

∴△ABD≌△DCE（AAS）；

（3）当∠BDA的度数为110°或80°时，△ADE的形状是等腰三角形，

∵∠BDA=110°时，

∴∠ADC=70°，

∵∠C=40°，

∴∠DAC=70°，

∴△ADE的形状是等腰三角形；

∵当∠BDA的度数为80°时，

∴∠ADC=100°，

∵∠C=40°，

∴∠DAC=40°，

∴△ADE的形状是等腰三角形．

【练2】阅读材料：小胖同学遇到这样一个问题，如图1，在△ABC中，∠ABC＝45°，AB＝2，AD＝AE，∠DAE＝90°，CE＝，求CD的长；

小胖经过思考后，在CD上取点F使得∠DEF＝∠ADB（如图2），进而得到∠EFD＝45°，试图构建“一线三等角”图形解决问题，于是他继续分析，又意外发现△CEF∽△CDE．

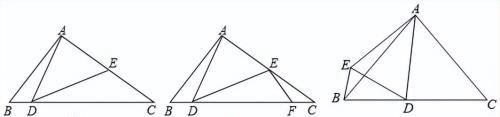
（1）请按照小胖的思路完成这个题目的解答过程．

（2）参考小胖的解题思路解决下面的问题：

如图3，在△ABC中，∠ACB＝∠DAC＝∠ABC，AD＝AE，∠EAD+∠EBD＝90°，求BE：ED．

【答案】CD=5；

（1）证明见解析；

（2）

【解析】解：（1）在CD上取点F，使∠DEF＝∠ADB，

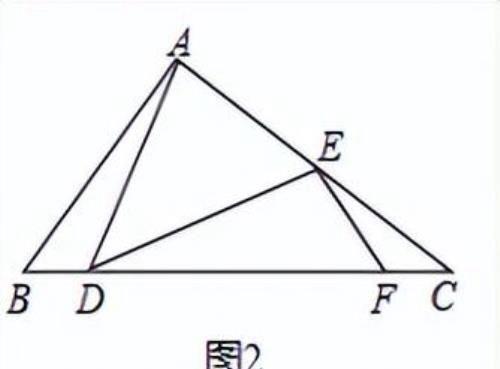
∵AD＝AE，∠DAE＝90°，

∴DE＝AD＝AE，

∵∠ABC＝45°，∠ADE＝45°，

且∠ADC＝∠ADE+∠EDC，

∴∠BAD＝∠EDC，

∵∠BDA＝∠DEF，

∴△ADB∽△DEF，

∴＝，

∵AB＝2，

∴DF＝4，

又∵∠CDE+∠C＝45°，

∴∠CEF＝∠CDE，

∴△CEF∽△CDE，

∴，

又∵DF＝4，CE＝，

∴，

∴CF＝1或CF＝5（舍去），

∴CD＝CF+4＝5；

（2）如图3，作∠DAT＝∠BDE，作∠RAT＝∠DAE，

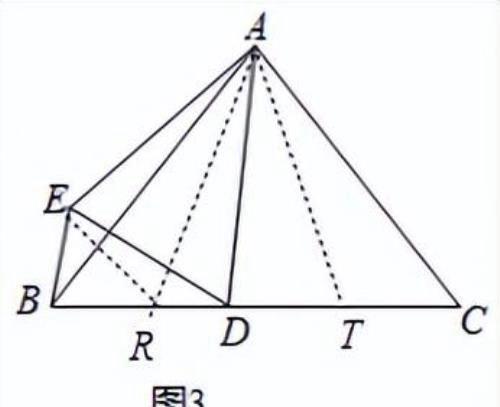
∵∠ACB＝∠DAC＝∠ABC，

∴AB＝AC，AD＝CD，

∵AD＝AE，

∴∠AED＝∠ADE，

∵∠EAD+∠EBD＝90°，

∴∠EAD+2∠EBD＝180°，且∠EAD+2∠AED＝180°，

∴∠EBD＝∠AED＝∠ADE，

∵∠BDA＝∠DAT+∠ATD＝∠BDE+∠ADE，

∴∠ADE＝∠ATD＝∠EBD，且∠BDE＝∠DAT，

∴△DBE∽△ATD，

∴，∠ADT＝∠BED，

∴，且AD＝DC，

∴，

∵∠RAT＝∠DAE，∠ADE＝∠ATD，

∴∠RAE＝∠DAT，∠AED＝∠ART＝∠ADE＝∠ATD，

∴AR＝AT，且∠RAE＝∠DAT，∠ARE＝∠ATD，

∴△ARE≌△ATD（ASA）

∴∠ADT＝∠AER，DT＝ER，

∴∠BED＝∠AER，

∴∠AED＝∠BER＝∠EBD，

∴RE＝RB＝DT，

∵AB＝AC，∠ABC＝∠ACB，∠ARB＝∠ATC，

∴△ABR≌△ACT（AAS）

∴BR＝TC，

∴DT＝TC，

∴CD＝2DT，

∴＝

【练3】数学模型（“一线三等角”模型）

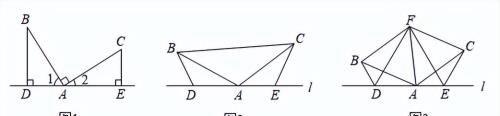
(1)如图1，∠BAC＝90°，AB＝AC，BD⊥AD于点D，CE⊥AD于点E．求证：△ABD≌△CAE．

(2)如图2，在△ABC中，AB＝AC，点D，A，E都在直线l上，并且∠BDA＝∠AEC＝∠BAC＝α．若CE＝a，BD＝b，求DE的长度（用含a，b的代数式表示）；

(3)如图3，D，E是直线上的动点，若△ABF和△ACF都是等边三角形，且∠BDA＝∠AEC＝∠BAC＝α，试判断△DEF的形状，并说明理由．

【答案】(1)见解析

(2)a+b

(3)△DEF是等边三角形，理由见解析．

【解析】(1)证明：∵∠1+∠2＝∠2+∠C＝90°，

∴∠1＝∠C，

在△ABD和△CAE中，

，

∴△ABD≌△CAE（AAS），

(2)解：∵∠BDA＝∠BAC＝α，

∴∠DBA+∠BAD＝180°﹣α＝∠BAD+∠CAE，

∴∠CAE＝∠ABD，

在△ABD和△CAE中，

∴△ABD≌△CAE（AAS），

∴AD＝CE，BD＝AE，

∵CE＝a，BD＝b，

∴DE＝AD+AE＝BD+CE＝a+b；

(3)解：△DEF是等边三角形，理由如下：

∵△ABF和△ACF都是等边三角形

∴AB＝AC，

由（2）知：△ABD≌△CAE，

∴BD＝AE，∠ABD＝∠CAE，

∵△ACF是等边三角形，△ABF是等边三角形，

∴∠CAF＝60°，AB＝AF，

∴∠ABD+∠ABF＝∠CAE+∠CAF，

即∠DBF＝∠FAE，

在△BDF和△AEF中，

，

∴△BDF≌△AEF（SAS），

∴DF＝EF，∠BFD＝∠AFE，

∴∠DFE＝∠AFD+∠AFE＝∠AFD+∠BFD＝60°，

∴△DEF是等边三角形．

【练4】数学模型学习与应用．【学习】如图1，，，于点C，于点E．由，得∠1=∠D；又，可以通过推理得到≌．我们把这个数学模型称为“一线三等角”模型；

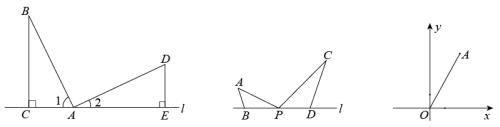
(1)【应用】如图2，点B，P，D都在直线l上，并且．若，，，用含x的式子表示CD的长；

(2)【拓展】在中，点D，E分别是边BC，AC上的点，连接AD，DE，，，．若为直角三角形，求CD的长；

(3)如图3，在平面直角坐标系xOy中，点A的坐标为，点B为平面内任一点．是以OA为斜边的等腰直角三角形，试直接写出点B的坐标．

【答案】(1)

(2)3

(3)或

【解析】

(1)解：∵，

∴，

∴，

又∵，

∴∽，

∴，

即，

∴．

(2)解：如图4，当时，

∵，，

∴∽，

∴，

∵，

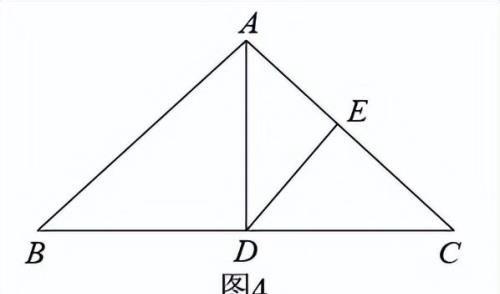
∴点D为BC的中点，

∴．

如图5，当时，

∵，

∴，

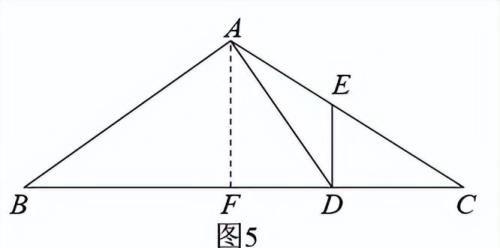
过点A作，交BC于点F，

∴，，

，不合题意，舍去，

∴．

(3)解：分两种情况：

①如图6所示，过A作AC⊥y轴于D，过B作BE⊥x轴于E，DA与EB相交于C，则∠C＝90°，∴四边形OECD是矩形

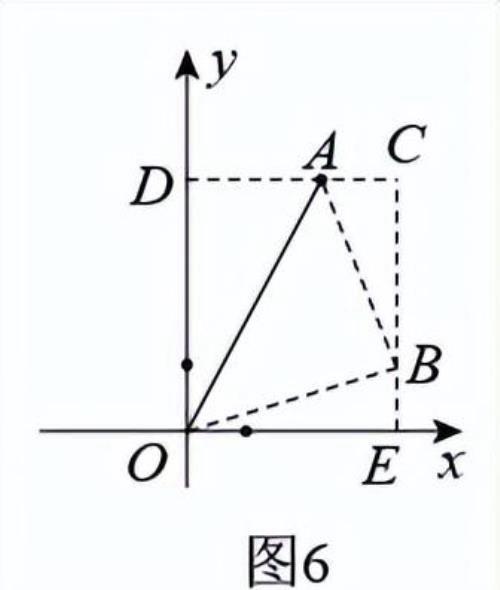
∵点A的坐标为（2，4），

∴AD＝2，OD＝CE＝4，

∵∠OBA＝90°，

∴∠OBE+∠ABC＝90°，

∵∠ABC+∠BAC＝90°，

∴∠BAC＝∠OBE，

在△ABC与△BOE中，

∴△ABC≌△BOE（AAS），

∴AC＝BE，BC＝OE，

设OE＝x，则BC＝OE＝CD＝x，

∴AC＝BE＝x－2，

∴CE＝BE+BC＝x－2+x＝OD＝4，

∴x＝3，x－2＝1，

∴点B的坐标是（3，1）；

②如图7，同理可得，点B的坐标（－1，3），

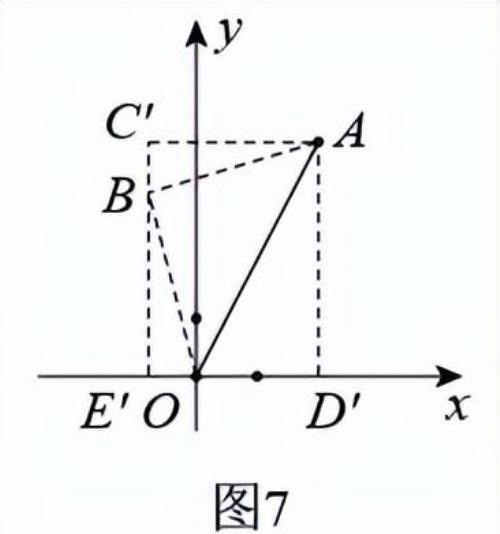
综上所述，点B的坐标为（3，1）或（－1，3）．

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小涵创作整理编辑！