线性代数中特征值和特征向量的意义(特征值与特征向量求法详解)

导语：趣味线性代数（八），特征值和特征向量

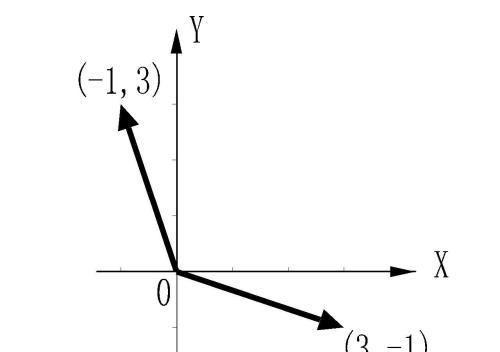
给出两个向量（3，-1）、（-1，3），如下图：

现在，我们玩个小游戏，按住向量（3，-1）的Y轴坐标不动，随意改变它的X轴坐标，相当于下图中的箭头在直线Y=-1上滑动；按住向量（-1，3）的X轴坐标不动，随意改变它的Y轴坐标，相当于下图中的箭头在直线X=-1上滑动。问，如果两个箭头滑动的正负方向和数量是相同的，有没有可能两条向量线段变为共线？

如上图，滑动后的向量线段为（3-t，-1）、（-1，3-t）。要判断两者能不能共线，只要使两者的斜率相等，即（3-t）/-1=-1/（3-t），再看看t有没有解就可以了。解得。

写到这里，我们可以引入特征值和特征向量的定义了。

设是阶方阵，如果数和n维非零向量x使关系式成立，那么，这样的数称为方阵的特征值，非零向量称为对应于特征值的特征向量 。

式，也可以写作。

可以看得出来，特征值就是上面提到的未知数。

同时，是包含两种未知量（特征值和特征向量）的齐次线性方程组，但是，因为中非零向量，则有行列式。

这是一件很有趣的事情，齐次线性方程组中另外包含着一个一元多次方程，这就使得整体求解的过程变得简单了。

例： 求矩阵

的特征值和特征向量。

解：A的特征多项式为

解得A的特征值为，。

对应地，求得基础解系：

所以是对应于的全部特征向量；是对应于的全部特征向量。

结构抗震计算是特征值与特征向量的应用场景之一。

已知无阻尼多自由度振动方程：

设的解为，那么

两式代入振动方程，化简得：

这样，求解振动方程就转化为求特征值与特征向量了。

本文内容由小梓整理编辑！