阿基米德折弦定理怎么证明(阿基米德折弦原理)

导语：超级经典，圆中阿基米德折弦定理六种证明方法及其练习

阿基米德(Archimedes，公元前287~公元前212年，古希腊)是有史以来最伟大的数学家之一。他与牛顿、高斯并称为三大数学家。

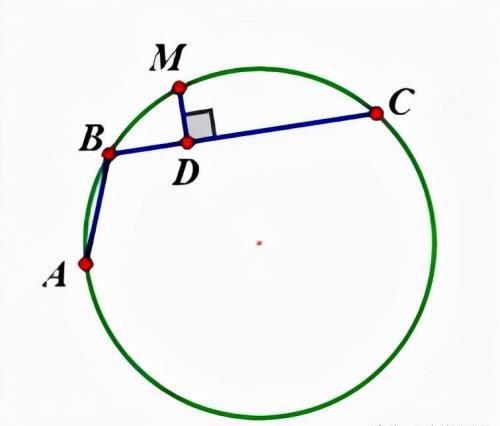
定理定义

如右图所示，AB和BC是⊙O的两条弦(即ABC是圆的一条折弦)，BC>AB，M是弧ABC的中点，则从M向BC所作垂线之垂足D是折弦ABC的中点，即CD=AB+BD。

定义:从圆周上任一点出发的两条弦，所组成的折线，我们称之为该图的一条折弦。

验证推导

方法1：补短法1

如图，延长DB至F，使BF=BA

∵M是弧ABC的中点

如图，延长DB至F，使BF=BA

∴∠MCA=∠MAC=∠MBC

∵MBAC四点共圆

∴∠MCA+∠MBA=180°

∵∠MBC+∠MBF=180°

∴∠MBA=∠MBF

∵MB=MB,BF=BA

∴△MBF≌△MBA

∴∠F=∠MAB=∠MCB

∴MF=MC

∵MD⊥CF

∴CD=DF=DB+BF=AB+BD

方法2：补短法2

延长AB到E，使BE=BD

∵M是弧AB中点，

∴∠MBC=∠MAC=∠MCA

∵M,B,A,C四点共圆

∴∠MCA+∠MBA=180°

∵∠MBE+∠MBA=180°

∴∠MCA=∠MBE

∴∠MBC=∠MBE

∵BE=BD,MB=MB

∴△EBM≅△DBM

∴∠E=∠MDC=90°,ME=MD

又∵MA=MC

∴△MEA≅△MDC

∴DC=AE=AB+BE=AB+BD

方法3:截长法1

如图，在CD上截取DG=DB

∵MD⊥BG

∴MB=MG，∠MGB=∠MBC=∠MAC

∵M是弧ABC的中点

∴∠MAC=∠MCA=∠MGB

即∠MGB=∠MCB+∠BCA=∠MCB+∠BMA

又∠MGB=∠MCB+∠GMC

∴∠BMA=∠GMC

∵MA=MC

∴△MBA≌△MGC(SAS)

∴AB=GC

∴CD=CG+GD=AB+BD

方法4:截长法2

如图，在CD上截取CG=AB

∵M是弧ABC的中点

∴MA=MC

∵∠BAM=∠BCM

∴△MBA≌△MGC(SAS)

∴MB=MG

∵MD⊥BG

∴BD=DG

∴CD=CG+GD=AB+BD

方法5:垂线法

如图，作MH⊥射线AB，垂足为H。

∵M是弧ABC的中点

∴MA=MC

∵MD⊥BC

∴∠MDC=90°=∠H

∵∠MAB=∠MCB

∴△MHA≌△MDC(AAS)

∴AH=CD，MH=MD

又∵MB=MB

∴Rt△MHB≌Rt△MDB(HL)

∴HB=BD

∴CD=AH=AB+BH=AB+BD

方法6：圆周角法

延长MD交圆O于E,连接EC,EA,

延长EA交CB延长线于F.

∵M为AMC中点

∴∠1=∠2

∵ MD⊥BC

∴∠EDF=∠EDC=90°,

∵ED=ED

∴△EDF≅△EDC

∴∠C=∠F,DF=DC

∵A.B,C,E 四点共圆

∴∠C+∠BAE=180°.

而∠3+∠BAE=180°

∴∠C=∠3

∴∠F=∠3

∴BF=AB

∴CD=FD=BF+BD=AB+BD

典例1 ☆☆☆☆☆

如图，已知点A，B，C，D顺次在圆O上，AB=BD，BM⊥AC，垂为 M.

证明∶AM＝DC＋CM.

1.（★★☆☆☆）如图，已知点 A，B，C，D顺次在圆O上，AB＝BD，BM⊥AC，垂足为 M.若 AM＝5，CM＝1，则 CD＝_______.

2.如图，已知△ABC中，D为AC上一点，且AD=DC+CB，过点D作AC的垂线交外接圆于点M.求证：M是优弧AB的中点．

3.如图，△ABC内接于⊙O，BC=2，AB=AC，点D为弧AC上的动点，

且cos∠ABC=

（1）求 AB 的长度.（2）求 AD· AE 的值.

（3）过A点作 AH⊥BD，求证∶BH=CD＋DH.

本文内容由小美整理编辑！