二次函数和等腰三角形技巧(二次函数构造等腰三角形问题)

导语：九年级数学：二次函数，一次函数，等腰三角形存在性，分类讨论

香雪海教育

题目呈现：

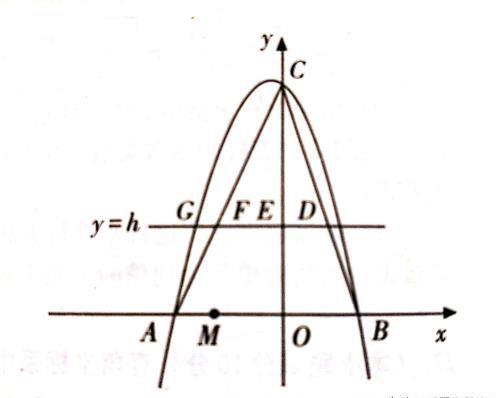
如图，在平面直角坐标系中，抛物线y=ax^2+bx+6经过点A（一3，0）和点B（2，0）。直线y=h（h为常数，且0<h<6）与BC交于点D，与y轴交于点E，与AC交于点F，与抛物线在第二象限交于点G。

（1）求抛物线的解析式。

（2）连接BE。求h为何值时，△BDE的面积最大。

（3）已知定点M（一2，0）。问：是否存在这样的直线y=h，使△OMF为等腰三角形？若存在，请求出h的值和点G的坐标；若不存在，请说明理由。

解析：

（1）将点A、点B的坐标代入抛物线解析式中，得二元一次方程组9a一3b+6=0，4a+2b+6=0。联解，得a=一1，b=一1。故抛物线的解析式为y=一x^2一x+6。

（2）欲求S△BDE，需知ED之长及其对应高之值。

∵直线y=h平行于x轴，EO⊥x轴，

∴ED边上的高=EO=yE=h。

易知点C坐标为（0，6），又已知点B（2，0），故可确定直线BC的解析式为y=一3x+6。

∵yD=yE=h，

∴xD=（6一h）/3=ED。

于是S△BDE=1/2×（6一h）/3×h=一1/6（h一3）^2+3/2。

显然，当h=3时，S△BDE最大=3/2。

（3）存在符合题意的直线y=h。

欲判定△OMF为等腰三角形，需知其各边长，进而确定h的值及点G坐标。

由点A（一3，0）及点C（0，6），可确定直线AC的解析式为y=2x+6。

∵yF=EO=h，

∴xF=（h一6）/2。

下面分别确定△OMF各边之长。

在△OFM中，OM=丨xM丨=2。

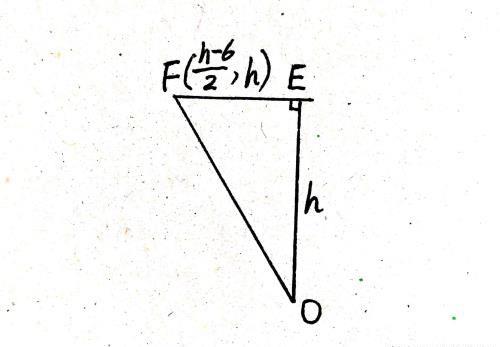
如下图所示，在Rt△OEF中，由勾股定理得OF=√（OE^2+EF^2）=√[h^2+丨（h一6）/2丨^2]。

如下图所示，作Rt△MFN，MN=丨xF一xM丨=丨xM一xF丨=丨（h一6）/2+2丨，FN=h。故MF=√{[丨（h一6）/2+2丨]^2+h^2}=√{[（h一2）/2]^2+h^2}。

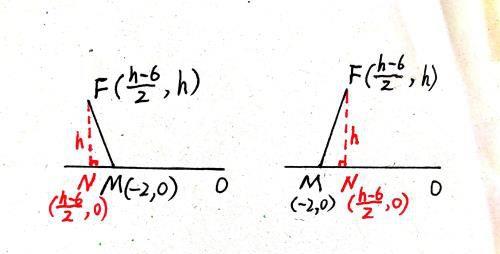
△OMF为等腰三角形，有三种可能：

①当MF=OM时，即√{[（h一2）/2]^2+h^2}=2，则h=2或h=一6/5（舍去，∵0<h<6）。

∵点G在抛物线上，且yG=h=2，

∴一x^2一x+6=2，解之得x1=（一1一√17）/2，x2=（一1+√17）/2>0，不在第二象限，舍去。

∴此时点G为（（一1一√17）/2，2）。

②当OF=MF时，即√{[（h一6）/2]^2+h^2}=√{[（h一2）/2]^2+h^2}，则h=4=yG。

∴一x^2一x+6=4，解之得x1=一2，x2=1（舍去）。

∴此时点G为（一2，4）。

③当OF=OM时，即√{[（h一6）/2]^2+h^2}=2，5h^2一12h+20=0，△=（一12）^2一4×5×20=一256<0，故此方程无解。

∴此时也不存在相应的点G。

总之，存在直线y=2或y=4，使△OMF为等腰三角形。当h=2时，点G为（（一1一√17）/2，2）；当h=4时，点G为（一2，4）。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小蔼创作整理编辑！