转圈追击问题(转圈相遇问题)

导语：关于转圈追及问题的奥数题，如何讲给小朋友？

奥数是培养逻辑推理能力和空间想象能力的最好办法。奥数教育是一个持之以恒的过程，每天练习才是关键。因此，家长才是奥数学习最好的老师。

今天的目标是让小朋友练习并讲解第9届华杯赛中关于转圈追及问题的一道奥数题，所用知识不超过小学4年级。

题目（难度：超五星压轴题）

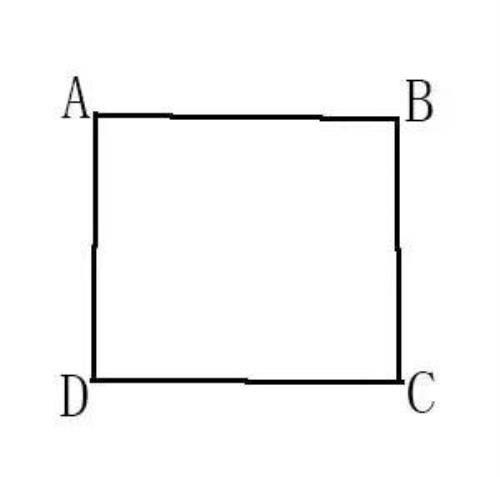
如图，正方形跑道ABCD上，甲乙丙3人同时从A点出发，顺时针跑步，3个人的速度分别为每秒钟5米、4米和3米。一段时间后，甲第一次看到乙和丙与自己处在正方形的同一条边上，且乙和丙都位于甲的前方。又过了21秒，甲乙丙3人相遇了。请问正方形的周长可能是多少？

答案：210米或420米

辅导办法:

将题目写给小朋友，让他自行思考解答，若20分钟还不能解答，由家长进行讲解。

讲解思路：

解决该题目，需要弄清楚三个问题，

一是甲第一次看到乙和丙与自己处在正方形的同一条边上时，甲在什么位置？

二是甲第一次看到乙和丙与自己处在正方形的同一条边上时，3个人之间的距离是多少？三是甲乙丙3人的相遇点在什么位置？

下面将分别分析这三个问题。

步骤1：

先思考第一个问题。

甲肯定是刚拐弯，位于ABCD的4个顶点中的某一个点，不然不会是第一次看到。

步骤2：

再思考第二个问题。

从甲第一次看到乙和丙与自己处在正方形的同一条边上，21秒之后，3个人相遇，

在这21秒内，甲跑105米，乙跑84米，丙跑63米，

说明第0秒，甲乙距离21米，甲丙距离42米。

步骤3：

再思考第三个问题，考虑3个人的相遇点。

分成甲乙2人和乙丙2人的相遇分别考虑，

甲的速度5，乙的速度4，甲跑5圈时，乙跑4圈，正好多了1圈。也就是说，甲乙人的相遇点都在出发点，即A点；

类似的，可以知道，乙丙2人的相遇点也都在A点。

因此，3人的相遇点一定是A点。

步骤4：

综合以上三个问题，

甲第一次看到乙和丙与自己处在正方形的同一条边上时，位于ABCD这4个点中的一个，21秒后，甲跑105米，就到达了A点；

且正方形的边长应该不小于甲和丙之间的距离，即不小于42米。

对甲的位置进行讨论：

若甲位于A点，则正方形周长是105米，边长只有26.25，小于42，不可能；

若甲位于B点，则正方形周长是140米，边长只有35，小于42，不可能；

若甲位于C点，则正方形周长是210米，边长52.5，大于42，可能；

若甲位于D点，则正方形周长是420米，边长有105，大于42，可能。

所以，正方形周长可能是210米或420米。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小纳创作整理编辑！