独立t检验怎么分析结果(独立t检验的作用)

导语：管理心理学之统计（12）独立测量的t分数

在之前章节中我们介绍的都是使用一个样本作为基础来推论有关总体的结论。如果涉及到两组或多组数据的平均数差异时会出现两种情况：

A. 两组数据来源于两个完全不同的样本，被称为独立测量研究设计或被试间设计。假设检验，允许实验者用来自两组独立样本的数据评估两个总体或两个处理条件的平均数差异。

B. 两组数据来源于同一个样本，是有关于重复测量研究的统计分析

今天我们来介绍第一种情况，独立测量研究设计（被试间设计）即每个处理条件或每个总体都应用单独样本的研究设计。

螺钉

1. 独立测量的假设检验

1.1 目的

独立测量检验假设的目的在于评价两个总体之间的平均数差。独立测验t分数用分别来自两个单独的样本的数据来决定两个总体或两个处理条件之间的差异是否显著。

1.2 步骤

A．提出假设

B．确定df, α水平，t分数临界值

C．计算合并方差，M2-M1的标准误，t值

在n1=n2的情况下，M2-M1的标准误为

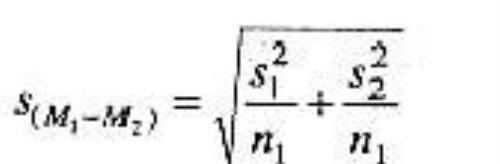
样本大小不对等时，就需要找到两个样本方差的准确平均值，即合并方差。

M2-M1的标准误为

t值为

当我们需要做减法来求得样本平均数的差时，独立测量t分数却要把两个样本的误差相加。如下图所示，在独立测量t分数中，需要通过计算变异性来找到一个样本平均数的差异，因此需要把每个样本平均数的变异性相加。

简单来说

总结为

D．得出结论

如果t在临界值之外，则拒绝假设H0

2. 独立测量的效应

2.1科恩d值

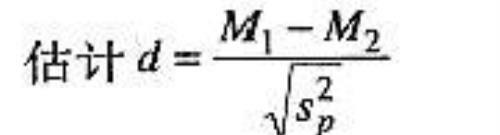
2.2方差百分比r2(解释变异性与总体变异性之间的百分比)

需要注意的是高的变异性使得到显著结果的可能性降低。合并方差小，两组数据重叠的部分小，差异性明显。合并方差大，重叠部分大，两组数据失去明显界限，差异不明显。

金属点阵字体字母 T 3d

3. 独立测量t分数公式的根本假设

3.1 根本假设

A．每个样本中的观察都必须是独立的。

B．两个样本相对应的两个总体必须是正态分布

C．方差齐性，即假设处理效果是给每个单个分数增加（或减少）一个常量。两个样本相对应的两个总体都必须有相等的方差。或者说只有两个样本都在估计相同总体的方差的时候，将这两个数值平均才有意义。在违反方差齐性的前提下得到一个极端t值，就会不知道两个值中的哪一个在起作用。

3.2 替代合并方差的方法（不需要满足齐性假设）

A. 通过单独方差计算标准误

B．调整t分数的自由度使df值变小，从而扩大了临界区域的边界线，使得检验更加苛刻，也因此纠正了合并方差想要校正的偏误问题

4. 如何检验是否满足方差齐性的假设-Hartley检验

如果两个总体方差是相等的，那么两个样本方差就应该近似。如果一个样本比另一个大三四倍，则合理怀疑不满足齐性假设。

步骤：A.为每个样本单独计算样本方差

B.计算方差中最大值和最小值的比例，Fmax

C. Fmax临界值表

手绘几何集

参考书目：行为科学统计，现代心理与教育统计学

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小梓创作整理编辑！