二元一次不等式平面区域怎么判断(二元二次不等式表示的平面区域怎么画)

对于高考，我们总是非常关心数学如何去考怎么考加上高考数学所要考查的知识点非常多，需要考生运用大量方法技巧进行解决问题，等等这些都增加高考数学的难度。

为了能帮助考生各个击破高考数学知识点，今天我们就来讲讲如何利用二元一次不等式来确定平面区域相关知识内容。

利用二元一次不等式确定平面区域相关问题，最大特点就是需要运用数形结合的思想，灵活度较高，不仅要求考生有扎实的计算功底，更要掌握好几何基本图形、平面直角坐标系相关知识内容。

下面让我们一起来看看高中数学大纲对二元一次不等式确定平面区域的具体要求：了解二元一课次不等式的几何意义，能用平面区域表示二元一次不等式（组）。

从大纲中我们可以看到，高考数学对这一块知识重在运用能力的考查，大家除了掌握好基本知识内容，努力提高自身运用知识解决问题的能力。

我们知道，关于二元一次方程Ax＋＋C=0的解都在该方程表示的直线上，同时这条直线把整个坐标平面分成两部分，每部分区域都对应着一个二元一次不等式。

在平面直角坐标系中二元一次不等式(组)表示的平面区域，具体可以分成以下两种情况：

1、当Ax＋＋C＞0时，表示区域是直线Ax＋＋C＝0某一侧的所有点组成的平面区域，不包括边界直线。

2、当Ax＋＋C≥0时，表示区域是直线Ax＋＋C＝0某一侧的所有点组成的平面区域，包括边界直线。

3、不等式组时候，表示区域是各个不等式所表示平面区域的公共部分。

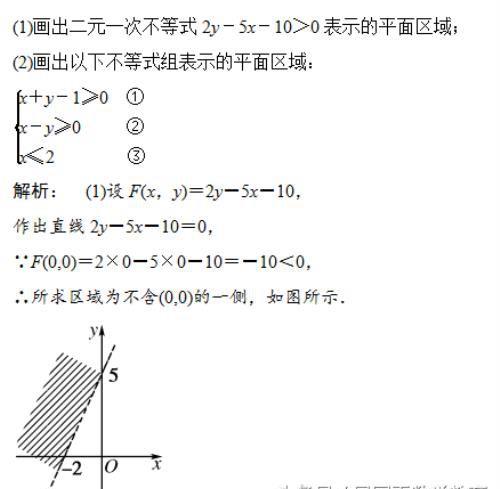
典型例题分析1：

解：(1)不等式x－y＋5≥0表示直线x－y＋5＝0上及右下方的点的集合．x＋y≥0表示直线x＋y＝0上及右上方的点的集合，x≤3表示直线x＝3上及左方的点的集合．

当x＝3时，－3≤y≤8，有12个整点；

当x＝2时，－2≤y≤7，有10个整点；

当x＝1时，－1≤y≤6，有8个整点；

当x＝0时，0≤y≤5，有6个整点；

当x＝－1时，1≤y≤4，有4个整点；

当x＝－2时，2≤y≤3，有2个整点；

所以平面区域内的整点共有2＋4＋6＋8＋10＋12＝42(个)．

在解题过程中，运用二元一次不等式来表示的平面区域的确定，需要注意以下这些事项：

二元一次不等式所表示的平面区域的确定，一般是取不在直线上的点(x0，y0)作为测试点来进行判定，满足不等式的，则平面区域在测试点所在的直线的一侧，反之在直线的另一侧。

二元一次不等式(组)表示平面区域的判断方法：直线定界，测试点定域。

注意：不等式中不等号有无等号，无等号时直线画成虚线，有等号时直线画成实线．测试点可以选一个，也可以选多个，若直线不过原点，测试点常选取原点。

典型例题分析2：

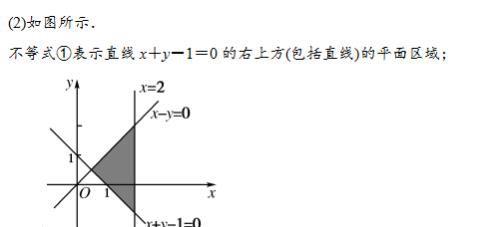
不等式②表示直线x－y＝0右下方(包括直线)的平面区域；

不等式③表示直线x＝2左方(包括直线)的平面区域．

所以，原不等式组表示上述平面区域的公共部分(阴影部分)．

最后大家一定要掌握好一些确定二元一次不等式表示平面区域的方法与技巧，如确定二元一次不等式表示的平面区域时，经常采用“直线定界，特殊点定域”的方法。

1、直线定界，即若不等式不含等号，则应把直线画成虚线；若不等式含有等号，把直线画成实线；

2、特殊点定域，即在直线Ax＋＋C＝0的某一侧取一个特殊点(x0，y0)作为测试点代入不等式检验，若满足不等式，则表示的就是包括该点的这一侧，否则就表示直线的另一侧。特别地，当C ≠0时，常把原点作为测试点；当C＝0时，常选点(1,0)或者(0,1)作为测试点。

免责声明:本文内容由互联网优秀作者用户自发贡献，本站仅提供存储空间服务，不拥有所有权,不承担相关法律责任。若有涉嫌抄袭侵权/违法违规的内容，请与我们取得联系举报，一经查实立刻删除内容。本文内容由快快网络小面创作整理编辑！