几何图形求面积的方法(几何图的面积)

导语：几何图形求面积，挑战一下吧

题目内容:如图所示:在矩形中，长为12，宽为8，连接长和宽的中点，求图中阴影部分面积是多少？

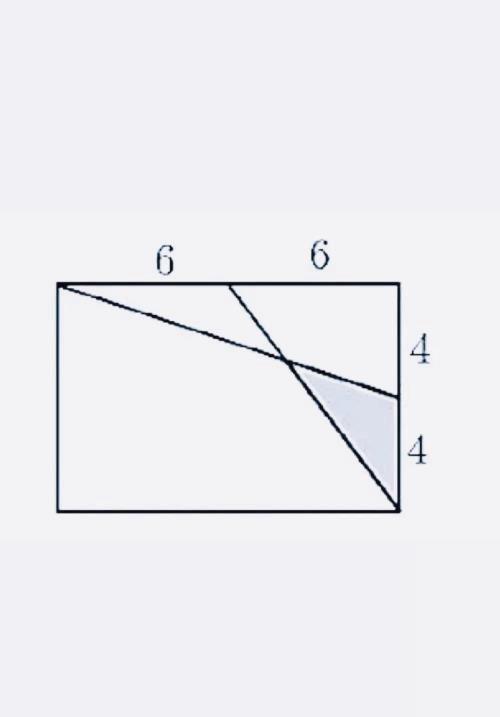
方法一:连结AC、EF，

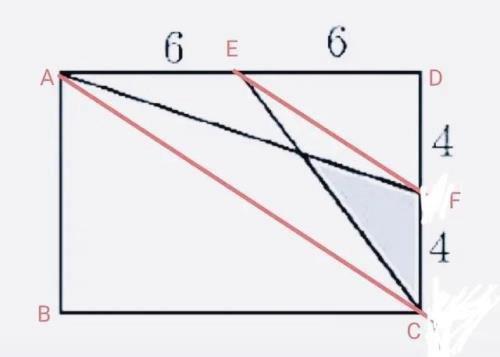
SΔACF＝4×(6+6)÷2=24，

SΔAEF＝6×4÷2=12，

这两个三角形AF同底，所以，AF边上的高比是2：1

SΔCEF＝12，所以，S阴影＝8

方法 二:

设阴影所在的直角三角形的顶点分別为A，B，C。阴影△其余的交点分别为D，E，交AB于D，交AC于E。C点D点都为所在边的中点。

S△ABC＝1／4S长＝（6十6）x（4十4）x1／4＝24。

阴影△ADE面积＝1／3S△ADE＝1／3×24＝8。

方法三:

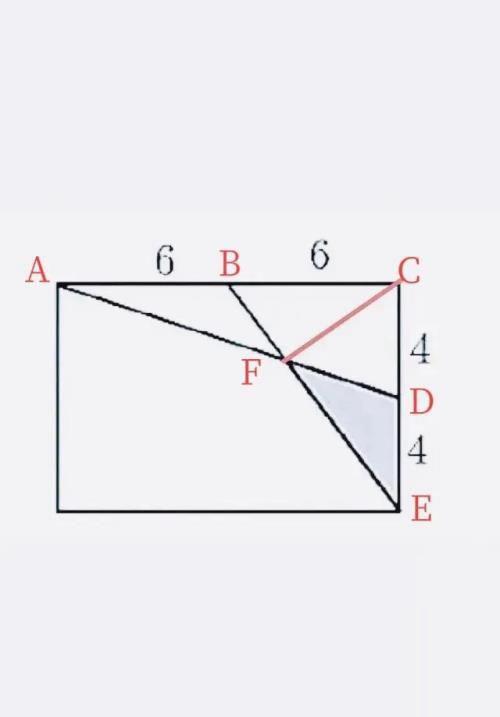
S△ACD=1/2x4×12,S△BCE＝1/2X8X6，通过计算可得两个三角形面积相等.

连接CF，又知BD为中点，易得阴影部分的面积是三角形面积的1/3.

S阴＝1/3x1/2x8X6＝8。

你还有什么好的方法呢？

欢迎留言评论！

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小春创作整理编辑！