从二次函数角度和二次方程的角度分别来证明什么(二次函数和角度问题)

导语：从二次函数角度和二次方程的角度分别来证明根的大小

题目很简单，就是证明一个二次方程有两个实数根，并且这两个根，一个比a大，一个比a小。首先，证明方程有两个不相等的实数根很简单，证明根的判别式大于0就可以了。现在主要是要证明两个根一个大于a，一个小于a。这道证明的重点其实是在这一个证明上。而实际上，就证明而言，也并不难理解，只是想通过这道题，来强化两种思想。一个是从二次函数的角度来看，通过数形结合的思想，把二次方程求根与二次函数根的分布结合起来，通过定义域与值域的关系来证明命题。另一个就是从纯二次方程的角度，通过根与根之间和、差、积、商等关系来证明命题。下面分别来看一下两种证法。

函数思想，在二次项系数为正，并且函数具有两个不相同实数根x1、x2的情况下，函数实际被分为三部分，当x<x1或者x>x2的情况下，函数值>0.当x1<x<x2的情况下，函数值<0。反之，当函数值>0时，我们可以推断x<x1或者x>x2成立，同理，当函数值<0的时候，那么x1<x1<x2也是成立的。这就是本题的证明思路，具体证明过程如下：

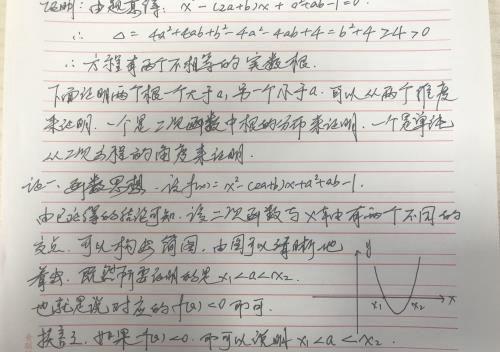
方程思想，既然是证明根的大小，那么就直接从根的关系来入手，首先通过求根公式，把两个根表达出来，然后通过处理，可以发现正好（x1-a）(x2-a)<0,进而说明x1-a与x2-a异号，从而证明结论。

其实，不管是函数思想，还是方程思想，都需要我们平时在做题的过程中，多多思考，多多总结。希望大家在学习的过程中，不要就题论题，而是可以发散思维，举一反三，在基础知识扎实的基础上，可以多联想，多思考，不断提高自己的数学素养。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小若创作整理编辑！