利用三垂线构造全等三角形(三条垂线交于一点怎么证)

导语：三条垂线引出的角度问题，如何找到全等是关键

请看题目：如图一，三角形ABC中，AD⊥BC，AD=BC，从三角形外两点M、N分别向BC作垂线，MB⊥BC，NC⊥BC，并且使得MB=CD, NC=BD，已知∠BAC=51°，求红色标记的∠MAN是多少度？

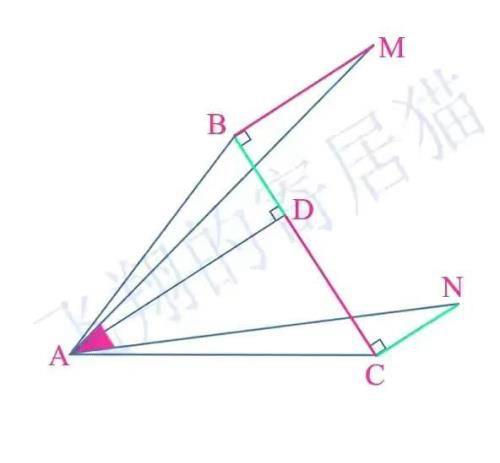
图一

这道题中可以看到有三组垂线，而且有三组线段的等量关系，那么线段相等，垂直90°角相等，那我们是否可以尝试构造全等三角形呢？比如AD=BC,BD=NC，两个直角，那么不就有“边角边”全等了吗？

如图二，如果连接NB，则三角形BNC和ADB全等，得到全等后，我们就可以得到对应的边和角也相等，即∠BAD=∠NBC，AB=NB，而∠BAD+∠ABD=90°，所以∠NBC+∠ABD=90°，这就意味着三角形ABN为等腰直角三角形，所以∠BAN=45°，而已知∠BAC=51°，所以∠NAC=51-45=6°

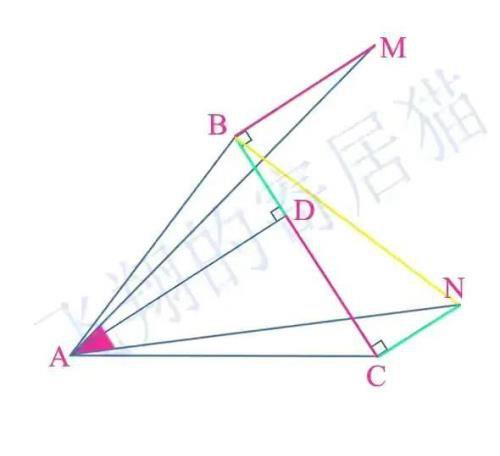
图二

按照这个思路，我们同样可以连接MC, 如图三，通过全等关系得到等腰直角三角形MCA，所以∠MAC=45°， 所以最终红色标记的∠MAN=∠MAC-∠NAC=45-6=39°

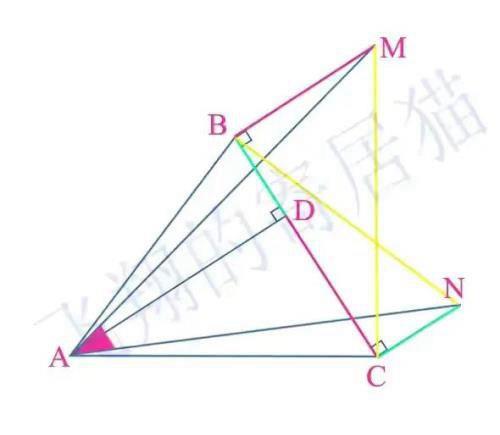
图三

如果大家还有更好的方法，欢迎一起来讨论分享！

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小梓创作整理编辑！