全等三角形的判定方法角角边(角角边证全等三角形)

导语：全等三角形判定之角边角、角角边定理的运用，找寻两者之间的异同

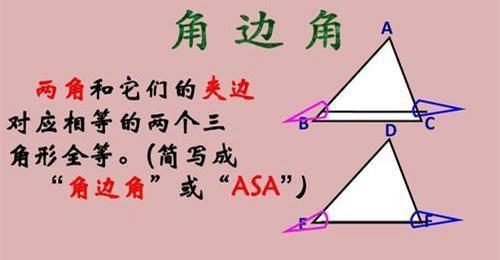
全等三角形判定定理中角边角定理和角角边定理非常的相似，角边角定理的内容是，两角和它们的夹边分别相等的两个三角形全等（ASA），角角边定理的内容是，两个角和其中一个角的对边对应相等的两个三角形全等（AAS）。

利用角边角定理判定两个三角形全等的条件是两角及这两个角的夹边对应相等，列举两个全等的条件时，要把夹边写在中间，同时注意挖掘隐含的等角，如：公共角、对顶角、平行线中的同位角、内错角等。而角角边定理的推导依据是根据三角形内角和定理和，因为三角形的内角和为180°，所以有两个角相等的话，第三个角也一定相等。所以“角角边”定理也可以看作是“角边角”定理的推论。这是两者之间的异同，书写格式上不同，但是却能够根据三角形内角和互相推导出来。也可以说“AAS”是“ASA”的一个推论。

例题1：如图，BE⊥AE，CF⊥AE,ME=MF,求证：AM是△ABC的中线。

【解析】：要证明AM是ABC的中线，就要证明BM=CM,要证明线段相等，就要证明与BM,CM有关的三角形全等，即△BEM≌△CFM，然后从已知条件中找出能够判断这两个三角形全等的条件.由题意知，BE⊥AE，CF⊥AE，得到∠BEM=∠CFM=90°,在△BME和△CMF中，∠BME=∠CMF，ME=MF,∠BEM=∠CFM,所以△BME≌△CMF(ASA)，所以BM=CM,所以AM是ABC的中线。

从本题中可以看出，在做证明题的时候，证明线段相等常用三角形全等，判定两个三角形全等，先根据已知条件或求证的结论确定三角形，然后再根据三角开全等的判定方法，看缺什么条件，再去证什么条件。也就是说，综合利用分析法和综合法寻找证明的途径。

关于全等三角形的判定的几种方法，一定要注意应用的条件，合理灵活的使用，对于证明题也要学会证明的途径，综合利用分析法和综合法最终证明出需要求证的结果。希望同学们多加练习，通过习题，总结出做题的规律和解题的思路，很多题目中有解题技巧，经过不断的积累，对于以后的综合类题目，运用起来就非常的顺畅了。加油

本文内容由小薇整理编辑！