与比例相关的等式与不等式的区别(与比例相关的等式与不等式有哪些)

导语：与比例相关的等式与不等式

引言：相似型，三角函数，是初三数学的主要内容。从全等到相似，边的关系则由绝对相等拓展至比例相等，因此有关比例的等量关系和不等关系就变得很重要了，是学生学习的一个重点也是难点，下面将常见的有关比例的关系总结一下。

首先还是由塞瓦定理的证明谈起，

塞瓦定理

【塞瓦定理及其逆定理】

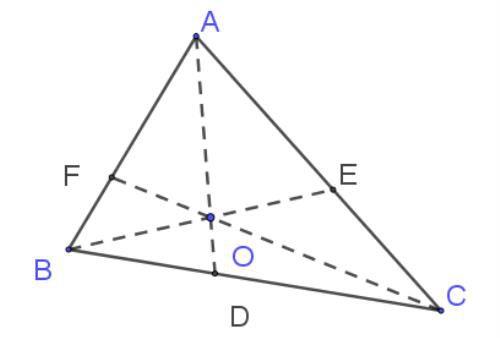
如图在中，AD，BE，CF相交于点O，则，

反之，若，则AD，BE，CF相交于一点。

在证明塞瓦定理时，需要由三条塞瓦线相交于一点推导上述比例式的乘积为1，证明过程是由面积出发得到的，其中

在这里用到了比例的一个性质：若，则，很多学生对有关比例的性质不太熟悉，在这里，本文将有关比例的性质罗列如下：若，则

（1）.（更比）；

（2）.(反比)；

（3）.（等比）

（4）.（合比），（分比）

（5）.（合分比）

在上述5个式子里，（1）（2）（4）（5）从代数上都很好证明，对于（5）式，只需将（4）式各项作比便可，对于第三个性质，则可从化学中浓度的角度和几何中向量或者斜率的角度取理解。

如图，

等比性质

从浓度的角度和几何的角度还可以得到以下不等关系：

（6）.（将咸淡程度不一的盐水混合后的浓度介于原两杯盐水的浓度之间），几何上如图所示

斜率不等式

最后，问大伙儿个问题：

若，则与的大小关系如何？

本文内容由小萱整理编辑！