圆内接三角形面积大值如何求(求圆内接三角形边长)

导语：一道高中题-求圆内接三角形的最大面积

一道高中题-求圆内接三角形的最大面积

已知一个圆的半径为1， 求这个圆的最大内接三角形的面积，并证明你的结论。

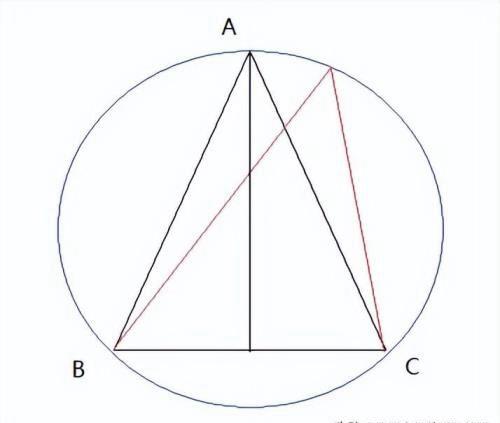
解：首先要证明对于同底来说，只有等腰三角形形才会有面积最大。

如图所示：等腰的时候有最大的高。

因此内接三角形至少是等腰三角形才有最大面积。

设底边BC=b, 圆的中心到底边的距离为X，如图示意：

根据勾股定理可以求出b用x表达的式子，

从而得出

这样三角形ABC的面积为

将b带入，

这相当于求上面函数的最大值，即求下列式子的最大值：

其中0≦x≦1,

若

对其求导：

对于0≦x≦1,

得出x=1/2, 有最大的三角形面积，这是因为在1/2的左侧的导数为正， 右侧为负，所以x=1/2为最大值点。

因此最大值的面积为

由上面的推导可以得出，圆内接等边三角形的时候有最大的三角形面积。

本文内容由小迪整理编辑！