傅里叶级数展开公式(傅里叶级数和傅里叶变换有什么关系)

导语：傅里叶级数

在我前面文章《伟大的数学家傅里叶》中，我们已经初步了解了傅里叶级数，今天还想和大家一起详细学习一下傅里叶级数。

一、三角级数

我们知道在科学实验与工程技术的某些现象中,常会碰到周期运动。最简单的周期运动,可用正弦函数y=Asin(ωx+φ)来描述,也称简谐振动,其中A为振幅,φ为初相角,ω为角频率,于是简谐振动y的周期是T=2π/ω。较为复杂的周期运动,则常常是几个简谐振动：

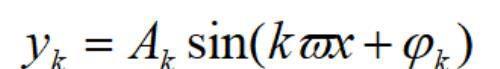
k=1,2,…,n的叠加

通过一系列的推导，我们可以得出更为一般的情况，即：

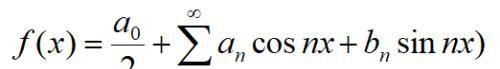
上式右边则称为三角级数。

组成三角级数的函数列1，cosx，sinx，cos(2x)，sin(2x)，…，cos(nx)，sin(nx)，…称为三角函数系。

三角函数系具有下面的性质：

1.三角函数系中所有函数有共同的周期2π。

2.在三角函数系中,任何两个不相同的函数的乘积在[-π,π]上的积分等于零,即：

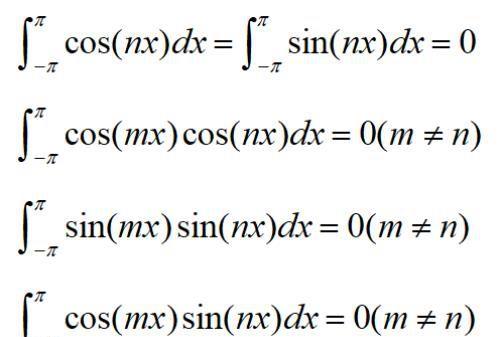
3.三角函数系中任何一个函数的平方在[-π,π]上的积分都不等于零。即：

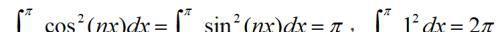
此性质说明三角函数系在[-π,π]上具有正交性,或者说是正交函数系。

二、傅里叶级数

有了上面的知识，我们便可以给出傅里叶级数的定义：设f(x)是周期为2π的周期函数，若

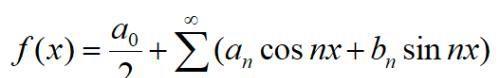
如果右边的三角级数在整个数轴上可积,则有如下关系式成立：

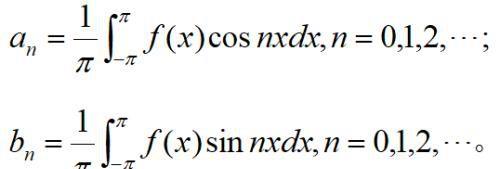
其中，an和bn称为函数f(x）关于三角函数系的傅里叶系数。

以f(x)的傅里叶系数为系数的三角级数称为f(x)的傅里叶级数,记作:

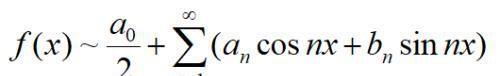
这里记号“～”表示上式右边是左边函数的傅里叶级数,若右边的三角级数在整个数轴上收敛于和函数f(x),根据定理,则此三角级数就是f(x)的傅里叶级数,即记号“～”可换为“=”。

按前述公式求出傅里叶系数并得到傅里叶级数,这时我们还需讨论：

(1)此级数是否收敛？

(2)如果收敛,是否收敛于f(x)本身？

此两个问题需要迪利克雷收敛定理回答。

迪利克雷定理：设f(x)是以2π为周期的函数，若该函数在闭区间[-π，π]上连续或只有有限个第一类间断点，并且至多只有有限个极值点,则f(x)的傅里叶级数收敛，进一步地，

(1)若x是f(x)的连续点，级数收敛于f(x)；

(2)若x是f(x)的间断点，级数收敛于f在点x的左、右极限的算术平均值,即：

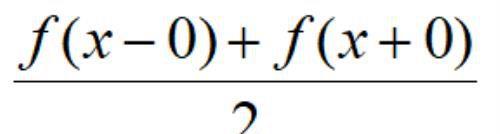
值得注意的是：尽管傅里叶级数的收敛性质不如幂级数,但它对函数的要求却比幂级数要低得多,所以应用更广。甚至函数周期性的要求也可以去掉。

三、正弦级数和余弦级数

一般地，若一个函数可以展开成傅里叶级数，其中既有正弦项，也含有余弦项。然而有些函数中只含正弦项或余弦项。事实上，这种现象与所给函数的奇偶性有关。这就是正弦级数和余弦级数。

设f(x)是周期为2π的函数，则有：

1.当函数f(x)为奇函数时，由于f(x)cos(nx)是奇函数，f(x)sin(nx)是偶函数，它们的积分偶倍奇零，则它的傅里叶系数为：

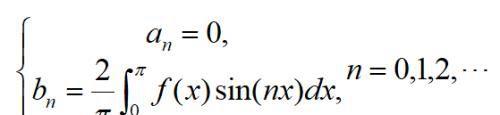
此时f(x)的傅里叶级数是只有正弦项的正弦级数。

2.当函数f(x)为偶函数时，则它的傅里叶系数为：

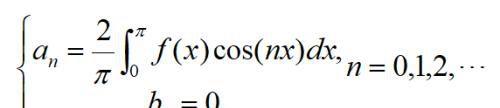
此时f(x)的傅里叶级数是只有常数项与余弦项的余弦级数。

对于在(0，π)上的函数f(x)，将其分别展开成正弦级数和余弦级数的步骤如下：

1.奇延拓。

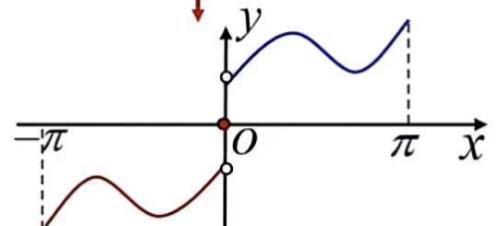
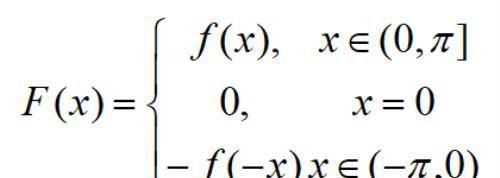
对F(x)进行周期延拓f(x)在(0，π]上展开成正弦级数。

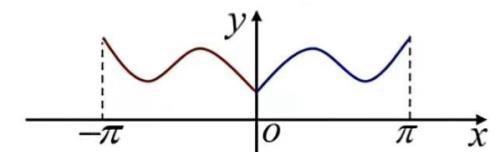
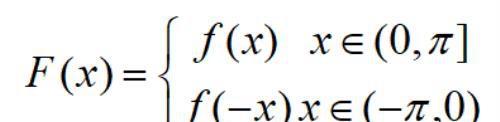
对F(x)进行周期延拓f(x)在(0，π]上展开成余弦级数。

四、周期为2l的函数的傅里叶级数

转换为傅里叶级数的函数周期不仅仅限于2π，可以是任意周期2L，只要对上述公式参数进行相应改变。

设f(x)是以2l为周期的函数,通过变量替换：

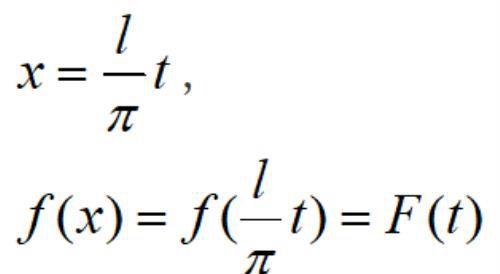
就可以将f(x)变换成以2π为周期的关于变量t的函数。若f在[-l,l]上可积,则F在[-π,π]上也可积,这时函数F的傅里叶级数展开式是：

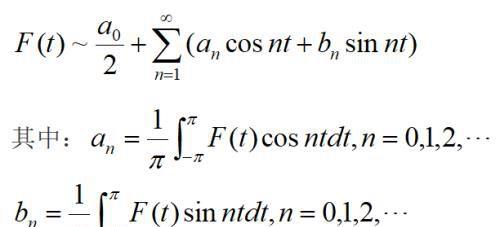
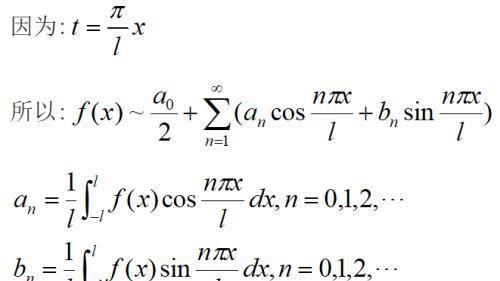
这是以2l为周期的函数f的傅里叶级数,an,bn是以2l为周期的函数f的傅里叶系数。

f(x)是以2l为周期的函数,若f在[-l,l]上满足迪利克雷收敛条件，则

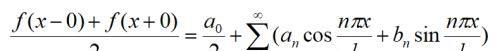
下面我们学习一个例子，加深我们对傅里叶级数的理解。

例：设f(x)在[0,π)上的表达式为：f(x)=1。

将f(x）进行奇延拓后‬，将‬f(x)展开成傅里叶级数。

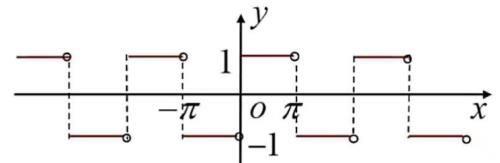
f(x)奇延拓图形

解：依题意，先求函数的傅里叶系数。

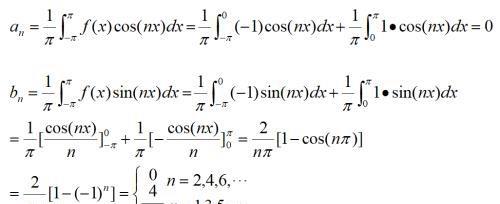
由于函数在点x=kπ（k=0，±1，±2，…）处是第一类间断点，在其他点处连续，根据定理知，当x=kπ时，该级数收敛于：

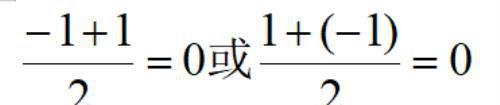
当x≠kπ时,有

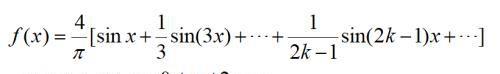
总之，傅里叶级数在实际中的应用主要是通过将复杂的周期函数表示成三角函数的线性组合，通过对简单函数的分析达到对复杂函数的深入理解和研究。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小曲创作整理编辑！