高中物理解决问题的三大方法(高中物理解题策略)

导语：解决50%高中物理问题的理论

如果让你说出高中力学最重要的理论是什么？相信凡是学过高中物理的都会给出自己的答案，这些答案中大部分都会包括：牛顿第二定律定律，动能定理，机械能守恒定律，动量定理，动量守恒定律这几个内容。为何？因为这就是高中物理力学的基本框架理论，把这几个理论吃透了，解决高中50%的问题是有基本保障的。

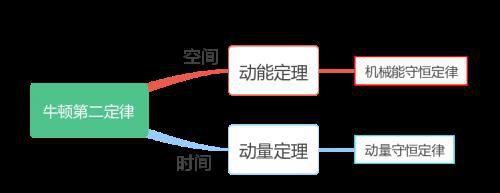
把这五个理论在同一张图（如下图）上表示出来，可以清晰地看出它们之间的关系。对于任何物理学问题，我们都会在空间与时间中进行考虑，牛顿第二定律中力在空间中进行累积得到功与动能变化量之间的关系，在限制做功的力（重力或弹力）的情况下进一步得到机械能守恒定律；力在时间上进行累积得到冲量与动量变化量之间的关系，同样在限制作用在系统上的力（内力）的情况下进一步得到动量守恒定律。

下面我们对这五个力学中最重要的理论及其之间的关系进行逐一分析。

一、牛顿第二定律

牛顿第二定律在力学中的重要地位不言而喻，高中物理教材不管是哪个版本，第一本要学的必然是以牛顿第二定律为核心的，整个课程的安排就是先研究匀变速直线运动，然后是相互作用力，接下来是牛顿运动定律，其基本逻辑都是先讲一个物理量加速度 a ,再讲物理量 F ,最后将加速度与力通过这一桥梁将与这两个物理量关联起来。

牛顿第二定律有以下几个性质：

1、矢量性

在牛顿第二定律中， 与 均为矢量，质量 为标量，表达式中的等号不仅表示数学上的大小相等的关系，还有方向相同的含义。由于 与 方向具有一致性，所以在有些问题中当物体的速度为零时，我们就可以根据物体的加速度进而求出对应的力。例如下面这个问题就应用到了牛顿第二定律的矢量性。

如图所示，一质量为的球由静止释放，求：球被释放的瞬间，其受到绳子的拉力大小为多少？

由于球在释放后会做圆周运动，所以其切向加速度一定与绳子垂直，刚释放的瞬间其速度为零，所以向心加速度也为零，这样球在释放的瞬间其加速度方向与绳子垂直，也就是合力的方向与绳子垂直。知道了合力与绳子的拉力的方向，重力的大小及方向，很容易就可以求出绳子拉力的大小为 。

2、瞬时性

与 是一对同时存在同时消失的物理量，也就是这两个物理量为物体同一时刻的瞬时加速度与受到的作用力。我们在在解决一类常见的问题——力的突变问题中就使用到了该性质，由于题目比较常见，在这里就不做举例。

3、因果性

牛顿第二定律的表达式其实我们看不出来与之间的因果关系，但是从文字表述“物体加速度的大小跟作用力成正比，跟物体的质量成反比，加速度的方向跟作用力的方向相同”中却可以很明显看出这一点，，也就是力是物体产生加速度的原因。在牛顿第二定律的验证实验中，我们通过控制变量法分别研究了 的关系，在保持质量 m 不变的情况下通过改变拉力 来测量出不同的 ，也说明了这两个物理量之间的关系是力的变化引起了加速度的变化，即力是因，加速度是果。

4、同一性

在应用牛顿第二定律进行分析物体运动时，我们做受力分析的第一步就是确定研究对象，为何？因为牛顿第二定律中的三个物理量对应着同一个物体，在同一惯性参考系中使用国际单位制进行分析。另外需要强调的是在受力分析的过程中一定要盯着研究对象进行分析，例如在使用整体法研究板块模型的过程中，老是有同学把当做整体的多个物体的总质量写成单个物体的质量，从而导致要么是加速度计算错误，要么是受力计算错误。

5、独立性

牛顿第二定律由于具有矢量性，其本质也就是数学中所说的向量，所以我们可以写成以下形式：

也就是说方向上的作用力只能产生方向上的加速度， 方向上的作用力只能产生 方向上的加速度，两个方向上的加速度与作用力之间是不会相互影响的。思考一个问题：在研究抛体运动的过程中为什么可以将物体的运动分解到两个互相垂直的方向上进行研究？原因就在于此性质。

牛顿第二定律在应用中常用来解决两大类问题，一类是已知加速度求力，另一类就是已知力求加速度，质量一般情况下是已知的，很少有题目会让求质量。但是需要注意的是这里所说的已知条件并不一定是题目中直接告诉你是多少，而是通过其他条件能够计算出来的隐含已知条件。适合应用牛顿第二定律分析的问题中物体绝大部分都是匀变速运动，包括匀变速直线运动与匀变速曲线抛体（抛体运动），而对于变加速直线运动与变加速曲线运动在做定量分析时基本是考虑某个瞬时或某个特殊位置的相关问题，比如在竖直平面内做变加速圆周运动物体都是要计算其最低点（或等效最低点）与最高点（或等效最高点）相关物理量。

二、动能定理

在分析动能定理之前我们考虑两个问题：

第一，功为什么要定义为 ?

第二，动能为何要定义为 ？

在回答这两个问题之前，我们先来分析一个具体的例子：

如图所示，一质量为 的物体在拉力 的作用下在光滑水平面上由左向右运动，其初速度为 ，末速度为 ,位移为 。由牛顿第二定律及匀变速直线运动的规律可得：

我们定义：为力对物体所做的功，为物体在某个瞬时或者某个位置处的动能，则可得出：

即物体所受合外力对物体所做的功等于物体动能的变化量。这里需要注意的是如果与 不在同一条直线上，那么功的表达形式则为 ，可以理解为，也可以理解为 ，即与 为同一方向上的物理量，要么将 分解到的方向上，要么将分解到的方向上。 为物体动量的变化量，需要注意的是一定是末状态的动能减去初状态的动能。

这时我们就可以回答开头提出的两个问题了，因为由牛顿第二定律及匀变速直线运动的规律我们推出了一个新的规律，我们给这个规律取个名教动能定理，给定理中出现的两个物理量分别取个名叫功，动能。可以将动能定理比作一个孩子，在孩子没出生之前我们是不会先给孩子取名的，因为孩子的性别及出生时辰不确定，没办法先取名的。

动能定理虽然是在匀变速直线运动的基础上推出来的，但是其应用范围却不限制在直线运动范围内，曲线运动同样适用。这一点我们可以从微元的角度去考虑。对于任何曲线运动，我们都可以将运动分解成许多很小的一段，每一小段都可以当做直线运动考虑：

运用动能定理解决的问题也是两种类型，一种是根据已知条件可以求出合外力做的功，然后再求出初状态或末状态的的速度大小；另一种则是根据已知条件先求出动能的变化量，然后再求出合外力做了多少功或某个力做了多少功。第一种问题牵涉到功的求解方法，包括恒力做功即变力做功的求解方法。恒力做功比较简单，只要根据功的定义进行计算即可，变力做功需要掌握微元法、图像法、平均法、转换法等特殊的方法，利用这些计算变力做功的特殊的方法将功表示出来再结合动能定理进行相关计算。

三、机械能守恒定律

在分析机械能守恒定律之前，我们先看两种情况：

1、只有重力做功

如图，一质量为 的物块距地面高度为 时，速度为 ,仅在重力作用下运动到距地面高度为 处，速度为 ，在此过程中，根据动能定理有：

定义：重力势能，则上式整理变形得：

2.只有弹力做功

一质量为 的物块在光滑水平面上在劲度系数为 的弹簧作用下做变加速直线运动，初速度为 ，末速度为，弹簧形变量分别为 ， ，由于弹簧弹力为变力,力与位移的关系为线性关系，所以使用平均法或图像法可以很容易计算出弹簧弹力对物块所做的功为：

再根据动能定理可得：

定义：弹性势能 ，则上式可整理为：

从已上两个实例中可以看出，在只有重力做功或只有弹力做功时，都有势能变化量与动能变化量之和为零，若将弹性势能 与重力势能 归为势能，即可以得到机械能守恒定律：

或

在推理的过程中我们我们可以看到只有重力或弹力对物体做功，涉及到的能量只有重力势能、弹性势能、动能三种能量，所以我们在利用机械能守恒定律前一定要使用以下三个条件判断机械能是否守恒：

只有重力或弹力对物体做功；除重力、弹力做功外，其他力做功代数和为零；只有重力势能、弹性势能、动能三种能量之间相互转化。

利用机械能守恒定律除了需要先判断机械能是否守恒，还要根据问题确定物体运动的初末两个状态的势能及动能分别如何表示。机械能守恒定律只关注初末两个状态，对于物体在初末两个状态之间的其他时刻是如何运动的是不需要做准确分析计算的。

四、动量定理

如图所示，一质量为的物体在拉力的作用下在光滑水平面上由左向右运动，其初速度为 ，末速度为 ,运动时间为 。由牛顿第二定律及匀变速直线运动的规律可得：

我们定义：冲量 ，动量 ，则可得出：

即合外力的冲量等于物体动量的变化量。冲量为矢量，同时也是过程量，动量也是矢量，由于速度是一个瞬时量，所以动量也是一个瞬时量，对应某个具体的时刻。从方程上看，该方程涉及到的物理量均为矢量，所以该方程为一个矢量方程，我们同样也可以将其分解到两个方向上：

动量定理不仅可以解决恒力作用下的运动学问题，同样也适用于变力作用下的运动学问题，特别是与电磁感应相关的问题及流体问题中解法单一，只能从动量的角度进行分析。

五、动量守恒定律

接下来我们分析如何运用动量定理推出动量守恒定律：

如上图所示，质量为的 A 物体初速度为，与质量为初速度为的 B 物体发生碰撞后速度分别变为 、 ，假设碰撞过程的A对B的平均作用力作用力为 ， B 对 A 的平均作用力为 ，碰撞时间为，分别用动量定理对 A 、 B 进行分析，可得：

将两式相加得：

又 与 为相互作用力，所以 ，所以

即:

更简洁的形式可以直接表示为:

虽然动量守恒定律在推导的过程中我们采用的是一位碰撞模型，但是其结论在二维或三维空间中仍然是适用的。在推理的过程中，系统中除了两物体之间的相互作用力外，其他力的冲量并没有考虑，这是因为物体受到其他力的合力为零，在运用动量定理时无需考虑。在运用动量守恒之前一定要从以下三个方面先确定动量是否守恒，即

系统不受外力作用；系统所受内力远大于系统所受到的外力作用；在某一个方向上满足已上两个条件之一，那么在该方向上动量守恒。

动量守恒定律在高考中只做一维要求，需要运用动量守恒定律的题目具有明显的特点，例如碰撞，爆炸，在某一方向上不受外力作用等。

六、五大理论的应用

前面着重从理论方面分析各个定理、定律及其之间的关系，这些定律、定理是我们解决力学问题最重要的工具，这也就是说，我们在解决力学问题时主要就是从牛顿第二定律、功能关系、动量三个角度进行思考。

牛顿第二定律一般用于解决恒力作用下的直线运动的问题，而功能关系及动量适用性更广，不仅能解决直线运动问题，同时能解决恒力或变力作用下的曲线运动的问题。很多同学在较复杂的力学问题时总是感觉到无从下手，对于经验丰富基本功底扎实的同学同学来说一眼就可以看出从哪个角度进行分析，对于经验不足的同学，由于总共也就三个思考维度，逐个维度去验证也未尝不是一种可行的方式。我们举个例子：

如图所示，在磁感应强度为 的匀强磁场中有一质量为 的导体棒放在光滑的水平轨道上，两轨道之间的距离为 ，左侧一阻值为 的电阻连接在两轨道之间。导轨及导体棒之间导线的电阻忽略不计，给导体棒一向右的初速度 ，求导体棒从开始运动至最终停下时的位移为多少？

在解题前我们要思考解题的思考方向，确定下来从哪个维度进行考虑。导体棒在磁场中运动切割磁感线产生感应电动势，又由于导轨、导体棒、电阻构成一个闭合回路，所以会产生感应电流 ，导体棒中有感应电流在磁场中就会受到向左的安培力 ，接下来会做减速运动。由于导体棒受到的安培力与速度相关，当速度减小时安培力也会减小，所以导体棒会做加速度减小的减速运动，其 图像为一曲线，我们无法利用高中知识求解处曲线下的面积——导体棒的位移，所以牛顿第二定律这条路肯定就走不通了。那么用动能定理呢？同样也不行。虽然我们知道了初末速度就知道了动能的变化量，但是安培力做功为变力做功，且力的大小与速度相关，而不是与位移相关，所以我们也无法把功表示出来。这样的话只能从第三个维度——动量的角度来思考解决这个问题。

使用动量时我们可以判断出系统动量肯定不守恒，所以只能使用动量定理进行分析：

设在很短的一段时间微元 内，导体棒的瞬时速度为 ，其受到向左的安培力为：

由动量定理可得:

在整个运动的过程中将所有的时间微元相加：

即导体棒从初始位置到最终停下来的位移为 。

至此，高中物理中的力学问题解题框架已经分析结束，接下来要做的就是在这些框架的基础上将常见的模型、解题方法、解题技巧进行归纳总结，并在平时练习时刻意去从这些角度去思考。如果已上所讲的要求都可以高水平地完成，所有的力学问题基本都可以迎刃而解！

本文内容由快快网络小婷创作整理编辑！