导语：每天一点土力学（25）：矩形面积竖向均布荷载作用下地基附加应力

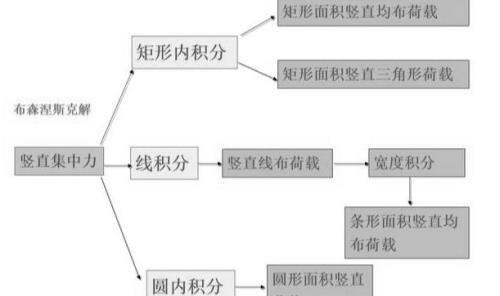
竖向集中力作用时地基附加应力

１）单个集中荷载作用下地基附加应力计算（布辛奈斯克解）

地基中附加应力是由建筑物荷载引起的应力增加，因此它是地基发生变形，引起建筑物沉降的主要原因。 法国 Ｊ．布辛奈斯克（Ｂｏｕｓｓｉｎｅｓｑ， １８８５）运用弹性理论推出了在弹性半空间表面上作用一个竖向集中力 P 时，半空间内任意点 M （x，y，z）处的 ６ 个应力分量和 ３ 个位移分量的弹性力学解答。（布辛奈斯克解较为复杂，具体参考相关教材）

２）不规则荷载作用下地基附加应力计算

在工程实践中，荷载很少是以集中力的形式作用在土体上，而往往是通过基础分布在一定面积上。 若基础底面的形状或基底下的荷载分布是不规则的，则可以把荷载面（或基础底面）分成若干个形状规则的单元面积（如图所示），

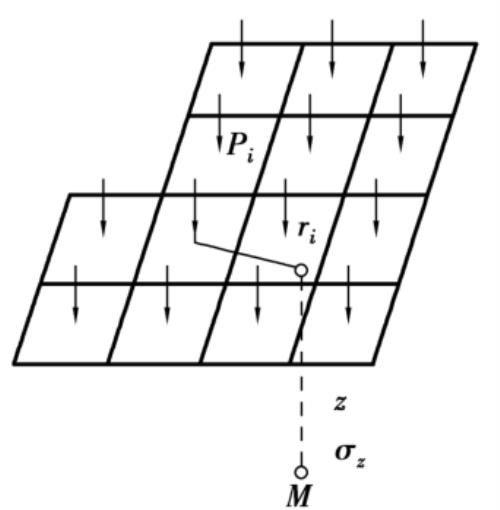
等代荷载法计算附加应力

每个单元面积上的分布荷载近似地以作用在单元面积形心上的集中力来代替，这样就可以利用布辛奈斯克公式和叠加原理计算地基中某点 M的附加应力。 这种近似方法的计算精度取决于单元面积的大小。 一般当矩形单元面积的长边小于单元面积形心到计算点距离的 １／２，１／３，１／４时，所算得的附加应力的误差分别不大于 ６％，３％和２％。如图所示的任一单元 i，可用集中力 P i 来代替单元面积上局部荷载。 在 P i 这个集中力作用下，地基中 M 点的附加应力为：

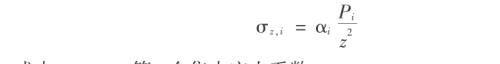
矩形面积竖向均布荷载作用下的地基附加应力

１）均布荷载作用下矩形面积角点下应力

矩形基础当底面受到垂直均布荷载作用时，基础角点下任意深度处的竖向附加应力，可利

用基本公式沿着整个矩形面积进行积分求得。设矩形荷载长度和宽度分别为 l 和 b，作用于

地基上的竖向均布荷载为 p ０ ，如图 所示。

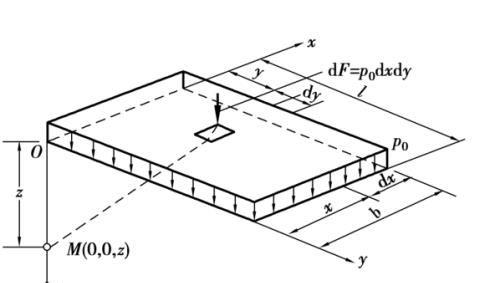
均布矩形荷载角点下的附加应力 σ

在矩形面积上取一微面积 ｄA ＝ｄxｄy，微面积上的合力 ｄF ＝p ０ ｄxｄy，其在角点 M 处产生的附加应力得

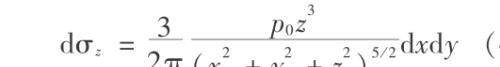
整个矩形面积上的均布荷载在 M 点所引起的附加应力，等于对上式在整个矩形荷载面 A 进行

积分：

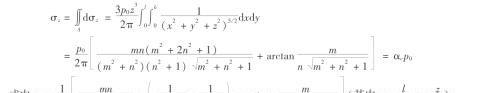
α ｃ 为矩形均布荷载角点下地基附加应力系数 m，n 的函数，可查表得。

２）均布荷载作用下矩形面积任意点下附加应力

求矩形面积受垂直均布荷载作用时地基中任一点的附加应力，可将荷载作用面积划分为几部分，每一部分都是矩形，并使待求应力之点处于划分的几个矩形的共同角点之下，然后利用上式分别计算各部分荷载产生的附加应力，最后利用叠加原理计算出全部附加应力，这种方法称为角点法。 角点法通常有以下 ４ 种情况：

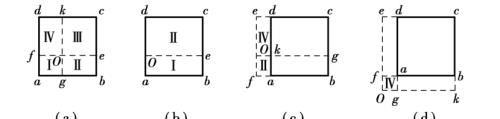
用角点法计算 O 点的附加应力

①O 点在荷载面内：

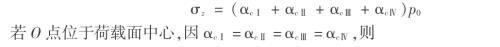
②O 点在荷载面边缘：

③O 点在荷载面边缘外侧：

④O 点在荷载面角点外侧：

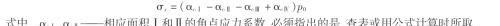
采用角点法计算应注意以下几点：

①划分的每一个矩形应有一个角点位于 M 点（计算点）；

②划分后用于计算的矩形面积总和应该等于原有受荷载面积，多算的应扣除；

③所划分的每个矩形面积，短边都用 b 表示，长边都用 l 表示。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小鸣创作整理编辑！