解反比例函数的题(如何解反比例函数)

导语：中考数学专题复习指导：学会解与反比例函数相关的动点问题

动点问题作为中考数学的热点和重点，每一位考生都很重视，都想通过复习彻底掌握好这一块知识内容。不过因动点问题内容过多，很多考生虽然花费大量时间和精力去复习，但总是很难找到相应的解题方法，帮助自己提高学习成绩。

关于动点问题，很多人都会先想到二次函数，而会忽视反比例函数知识的积累。

反比例函数虽然没有像二次函数那么出彩，但它毕竟是初中数学三大函数之一，在中考数学中还是占据着重要的位置，我们一定要认真对待，因此，今天我们就一起来讲讲与反比例函数相关的动点问题。

与反比例函数相关的动点问题，典型例题分析1：

如图，已知A、B是反比例函数y=k/x（k＞0，x＞0）图象上的两点，BC∥x轴，交y轴于点C．动点P从坐标原点O出发，沿O→A→B→C（图中“→”所示路线）匀速运动，终点为C．过P作PM⊥x轴，PN⊥y轴，垂足分别为M、N．设四边形OMPN的面积为S，P点运动时间为t，则S关于t的函数图象大致为（　 　）

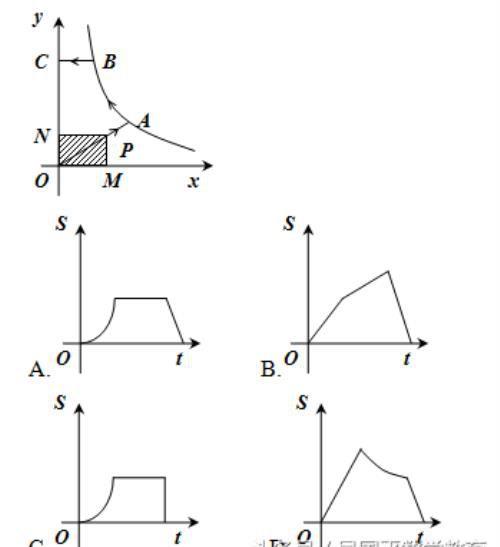
解：当点p在OA上运动时，此时S随t的增大而增大，当点P在AB上运动时，S不变，

∴B、D淘汰；当点P在BC上运动时，S随t的增大而逐渐减小，

∴C错误．故选A．

考点分析：

反比例函数综合题；动点问题的函数图象；综合题.

题干分析：

当点p在OA上运动时，此时S随t的增大而增大，当点P在AB上运动时，S不变，当点P在BC上运动时，S随t的增大而减小，根据以上判断做出选择即可。

解题反思：

本题考查了反比例函数的综合题和动点问题的函数图象，解题的关键是根据点的移动确定函数的解析式，从而确定其图象。

反比例函数和二次函数定义上虽然不同，但本质上都是函数，因此，与反比例函数相关的动点问题都需要找到相应的等量关系，建立函数解析式，通过函数的图像与性质把问题正确解决。

与反比例函数相关的动点问题，典型例题分析2：

在矩形AOBC中，OB=6，OA=4，分別以OB，OA所在直线为x轴和y轴，建立如图所示的平面直角坐标系．F是BC上的一个动点（不与B．C重合），过F点的反比例函数y=k/x（k＞0）的图象与AC边交于点E．

（1）求证：AE•AO=BF•BO；

（2）若点E的坐标为（2.4），求经过O．E．F三点的抛物线的解析式；

（3）是否存在这样的点F，使得将△CEF沿EF对折后，C点恰好落在OB上？若存在，求出此时的OF的长：若不存在，请说明理由．

考点分析：

相似三角形的判定与性质；反比例函数图象上点的坐标特征；待定系数法求二次函数解析式；矩形的性质；翻折变换（折叠问题）。

题干分析：

（1）根据反比例函数的性质得出，xy=k，即可得出AE•AO=BF•BO；

（2）利用E点坐标首先求出BF=4/3，再利用待定系数法求二次函数解析式即可；

（3）设折叠之后C点在OB上的对称点为C'，连接C'E．C'F，过E作EG垂直于OB于点G，则根据折叠性质．相似三角形．勾股定理得出即可。

解题反思：

此题主要考查了反比例函数的性质以及待定系数法求二次函数解析式以及相似三角形的判定与性质，二次函数的综合应用是初中阶段的重点题型特别注意利用数形结合以及利用相似三角形的性质是这部分考查的重点也是难点。

所谓＂动点问题＂是指题设图形中,存在一个或多个动点,它们在线段、射线或弧线上运动的一类开放性题目。解决这类问题的关键是动中求静,在变化中找到不变的性质。

与反比例函数相关的动点问题，典型例题分析3：

考点分析：

二次函数综合题，动点问题，曲线上点的坐标与方程的关系，对称的性质，线段中垂线的性质，含300角的直角三角形的性质，锐角三角函数定义，特殊角的三角函数值，点到直线的距离，二次函数的最值。

题干分析：

（1）抛物线的解析式中，令x=0，能确定抛物线与y轴的交点坐标（即B点坐标）；令y=0，能确定抛物线与x轴的交点坐标（即A、C的坐标）。

（2）由（1）的结果，利用待定系数法可求出直线AB的解析式。

（3）欲求出反比例函数的解析式，需要先得到D点的坐标．已知A、B的坐标，易判断出△OAB是含300角的直角三角形，结合O、D关于直线AB对称，可得出OD的长，结合∠DOA的值，应用三角函数即可得到D点的坐标。

（4）首先用t列出AQ、AP的表达式，从而可得到点P到x轴的距离，以OQ为底、P到x轴的距离为高，可得到关于S、t的函数关系式，根据函数的性质即可得到S的最大值及此时t的值。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小茹创作整理编辑！