虚拟线条(直线和虚线形成的算不算角)
导语:一轮复习:“直线边界”和“虚拟直线边界”粒子运动
带电粒子在直线边界的匀强磁场中运动,实际就是几何作图,本质就是直线与圆相交问题,也就是对称性。
在没有直线边界的匀强磁场中运动,也可以把起点和终点连接起来,构建一条虚拟的直线,此直线与速度的夹角也就是弦切角。
常用结论:
1.同一直线边界进出,速度和直线夹角相等。(但不平行,垂直进出除外)
2.该条直线其实就是弦,速度与直线的夹角就是弦切角
3.圆心角等于速度与直线夹角的2倍或者2(π-θ)。
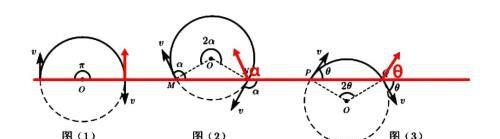
如图所示,粒子进出磁场具有对称性,且粒子以多大的锐角θ进人磁场,就以多大的锐角θ出磁场;粒子进入磁场时的速度v垂直边界时,出射点距离入射点最远,且Smax=2R,如图甲所示;同一出射点,可能对应粒子的两个入射方向,一个为“优弧”,另一个为“劣弧”,如图乙、丙中的出射点A.
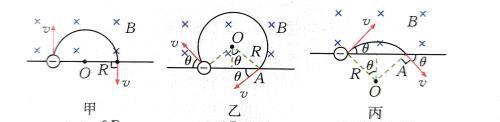
类型一:真实直线边界
【例题】如图所示,在直线MN的上方区域中有匀强磁场,磁感应强度为B.一个带电粒子以与磁场垂直的速度从a点进人磁场,从b点离开磁场。已知粒子的电荷量为q,质量为m,在a点速度与MN的夹角为θ.(B)
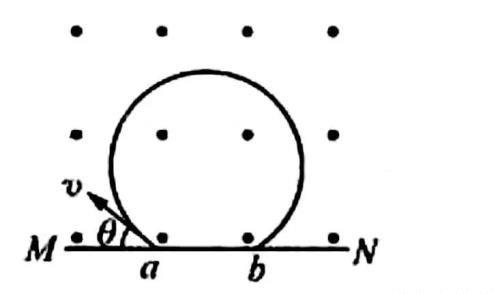
A.粒子带正电,它在磁场中运动的时间是2mθ/Bq
B.粒子带正电,它在磁场中运动的时间是2m(π一θ)/Bq
C.粒子带负电,它在磁场中运动的时间是2mθ/Bq
D.粒子带负电,它在磁场中运动的时间是2m(π一θ)/Bq
【解析】
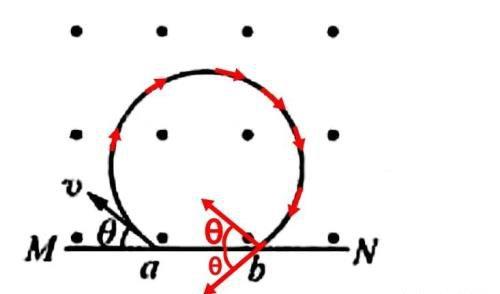
【例题】如图所示,在垂直纸面向里的匀强磁场的边界上,有两个质量和电荷量均相同的正、负离子,从O点以相同的速度射入磁场中,射入方向均与边界成θ角.若不计重力,关于正、负离子在磁场中的运动,下列说法正确的是(ABC)
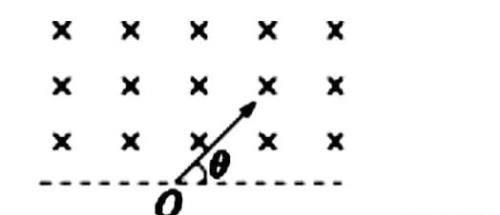
A.运动的轨道半径相同
B.重新回到边界的速度大小和方向都相同
C.重新回到边界的位置与O点距离相同
D.运动的时间相同
例题:如图所示,直角三角形ABC区域中存在一匀强磁场,比荷相同的两个粒子沿AB方向射入磁场,分别从AC边上的P、Q两点射出,则(BD)
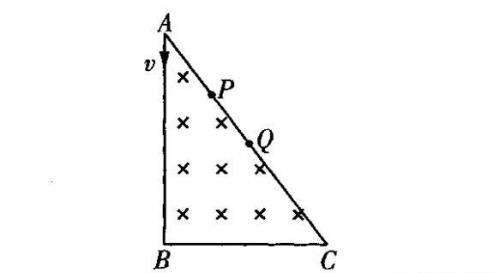
A.从P点射出的粒子速度大、
B.从Q点射出的粒子速度大
C.从P点射出的粒子在磁场中运动的时间长
D.两粒子在磁场中运动的时间一样
【解析】
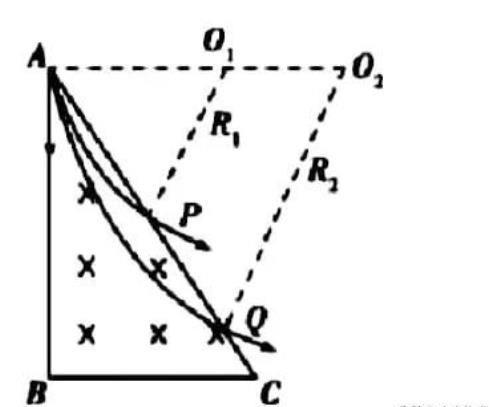
【例题】如图所示,在y<0的区域内存在匀强磁场,磁场方向垂直于xy平面并指向纸面外,磁感强度为B.一带正电的粒子以速度v₀从O点射入磁场,入射方向在xy平面内,与x轴正向的夹角为θ,若粒子射出磁场的位置与O点的距离为l,求该粒子的电量和质量之比q/m.
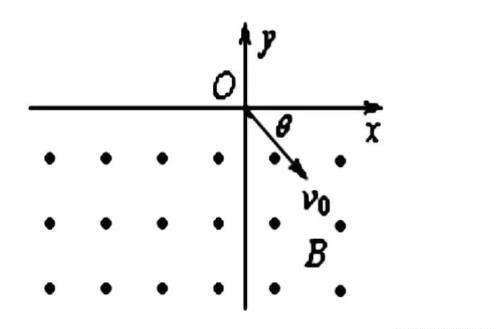
【解析】
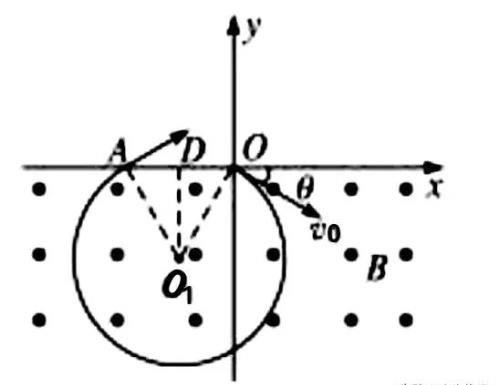
【答案】2v₀sinθ/Bl
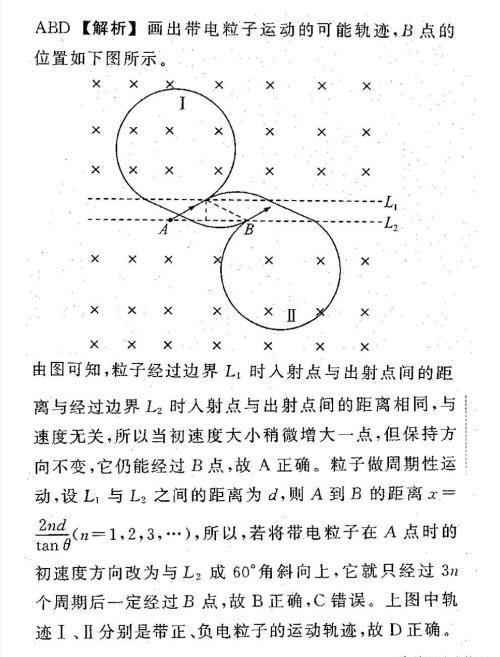
【例题】如图所示,L₁和L₂,为两平行的虚线,L₁上方和L₂下方都是范围足够大,且磁感应强度相同的匀强磁场,A、B两点都在L₂上.带电粒子从A点以初速度v₀与L₂成30°角斜向右上方射出,经过偏转后正好过B点,经过B点时速度方向也斜向上,不计重力,下列说法不正确的是()
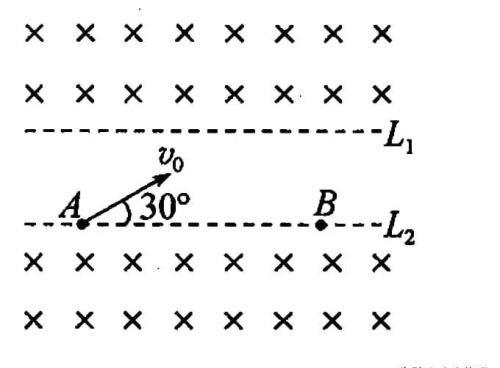
A.带电粒子经过B点时速度一定跟在A点时速度相同
B.若将带电粒子在A点时的初速度变大(方向不变),它仍能经过B点
C.若将带电粒子在A点时的初速度方向改为与L₂成60°角斜向右上方,它将不能经过B点
D.此粒子既可以是正电荷,也可以是负电荷
【例题】平面OM和平面ON之间的夹角为30°,其横截面(纸面)如图所示,平面OM上方存在匀强磁场,磁感应强度大小为B,方向垂直于纸面向外。一带电粒子的质量为m,电荷量为q(q>0)。粒子沿纸面以大小为v的速度从OM的某点向左上方射入磁场,速度与0M成30°角。已知该粒子在磁场中的运动轨迹与ON只有一个交点,并从OM上另一点射出磁场。不计重力,粒子离开磁场的出射点到两平面交线上O点的距离多少?
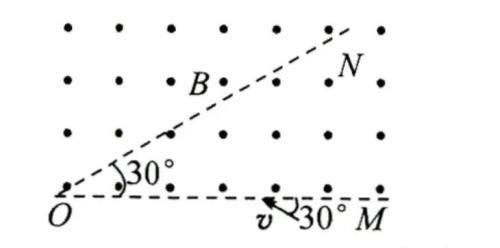
【解析】
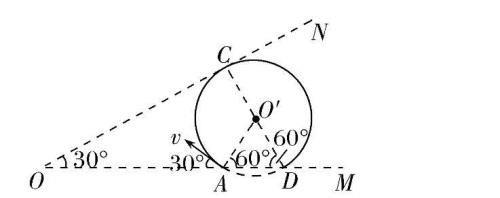
【答案】4mv/qB
【例题】如图所示,在坐标系xOy中,第一象限内充满着两个匀强磁场a和b,OP为分界线,磁场a的磁感应强度为2B,方向垂直纸面向里;磁场b的磁感应强度为B,方向垂直纸面向外,P点坐标为(4l,3l).一质量为m,电荷量为q的带正电的粒子从P点沿y轴负方向射入磁场b,经过一段时间后,粒子恰能经过原点O,不计粒子重力.(sin37°=0.6,cos37°=0.8)

求:
(1)粒子从P点运动到O点的时间最少是多少?
(2)粒子运动的速度可能是多少?

【例题】如右图所示,有一个正方形的匀强磁场区域abcd,e是ad的中点,f是cd的中点,如果在a点沿对角线方向以速度v射入一带负电的带电粒子,恰好从e点射出,则(AD)
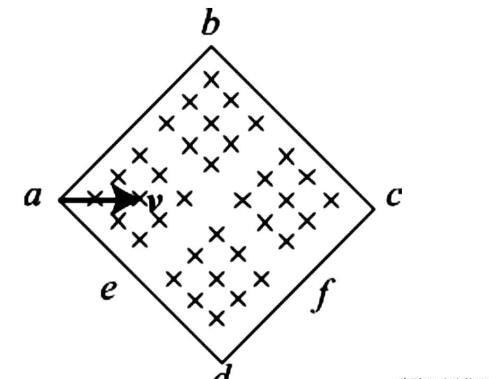
A.如果粒子的速度增大为原来的二倍,将从d点射出
B.如果粒子的速度增大为原来的三倍,将从f点射出
C.如果粒子的速度不变,磁场的磁感应强度变为原来的二倍,也将从d点射出
D.只改变粒子的速度使其分别从e、d、f点射出时,从f点射出所用时间最短
类型二:虚拟直线边界
例题:如图所示,

在一个边长为a的正六边形区域内存在磁感应强度为B,方向垂直于纸面向里的匀强磁场,带正电的粒子,比荷为q/m,先后从A点沿AD方向射入匀强磁场区域,粒子在运动过程中只受磁场力作用,粒子恰好从E点飞出磁场区域,求粒子在磁场区域内运动的时间。
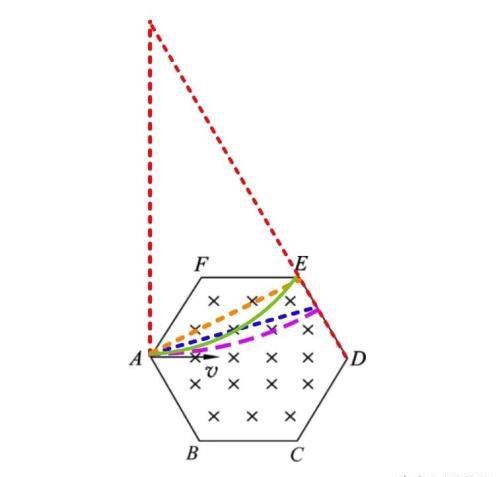
AE连接起来,构建一条虚拟的直线,实际也是弦,利用弦切角。t=πm/3qB
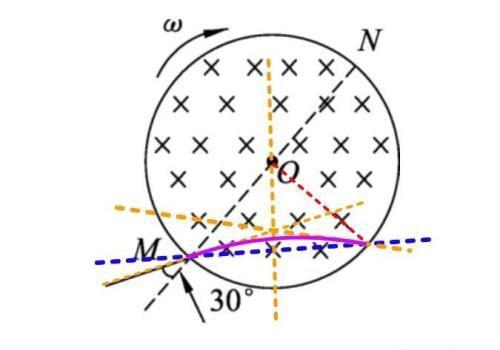
例题:一圆筒处于磁感应强度大小为B的匀强磁场中,磁场方向与筒的轴平行,筒的横截面如图所示.
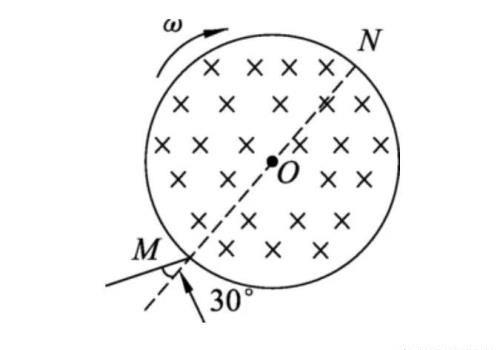
图中直径MN的两端分别开有小孔.筒绕其中心轴以角速度ω顺时针转动.在该截面内,一带电粒子从小孔M射入筒内,射入时的运动方向与MN成30°角.当筒转过90°时,该粒子恰好从小孔N飞出圆筒.不计重力.若粒子在筒内未与筒壁发生碰撞,则带电粒子的比荷为?
【解析】
构建一条虚拟直线,粒子在此直线上进出,速度夹角相等,偏转角为30°,运动时间为t=6πm/qB=π/2ω,得到q/m=ω/3B。
免责声明:本站部份内容由优秀作者和原创用户编辑投稿,本站仅提供存储服务,不拥有所有权,不承担法律责任。若涉嫌侵权/违法的,请反馈,一经查实立刻删除内容。本文内容由快快网络小梓创作整理编辑!