蝴蝶定理的证明过程(蝴蝶定理的证明方法)

导语：蝴蝶定理的证明

设M是一个圆的弦PQ的中点，通过它可以画出另外两个弦AB和CD;AD与PQ相交于X点, BC与PQ相交于Y点，证明M也是XY的中点。

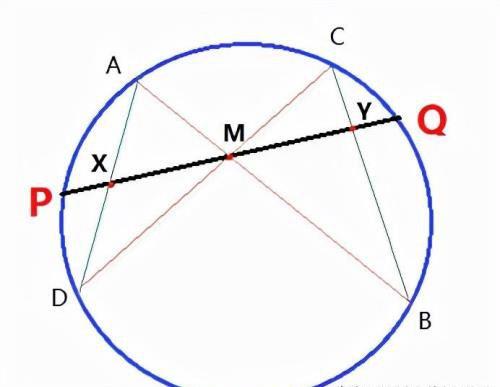
证明1：我们从X点做AB的垂直线段x1, 做CD的垂直线段x2；同时从Y点做AB的垂直线段y1, 做CD的垂直线段y2, l令MP=MQ=a， MX=x, MY=y.

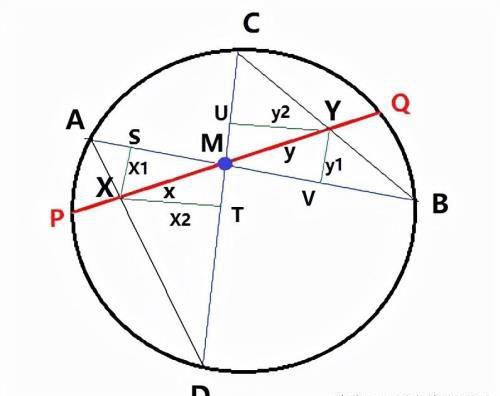
在上面的图形中，有多对直角三角形相似：

三角形s 相似比

MSX和MVY x/y = x1/y1

MXT和MYU x/y = x2/y2

AXS和UCY x1/y2= AX/CY

DXT和 BYV x2/y1= XD/YB

根据上面的等式有：

x²/y² = x1/y1· x2/y2

= x1/y2· x2/y1

=AX/CY·XD/YB

= AX·XD/ (CY·YB)

= PX·XQ/ (PY·YQ.) (这一步是圆内接四边形对角线的性质，对角线的交点分割成的各自对角线的两部分乘积相等，利用相似三角形即可证明)

将PX=a-x, XQ=a+x, PY=a+y, YQ=a-y带入：

x²/y² = (a - x)(a + x)/ (a - y)(a + y) = (a² - x²)/(a² - y²)

将等式化简后：

a²x²=/a²y²

所以x=y

证明2：为方便起见，请按照下图中的角度来表示。设x = XM, a = PM。在证明1中，我们已经说明了：

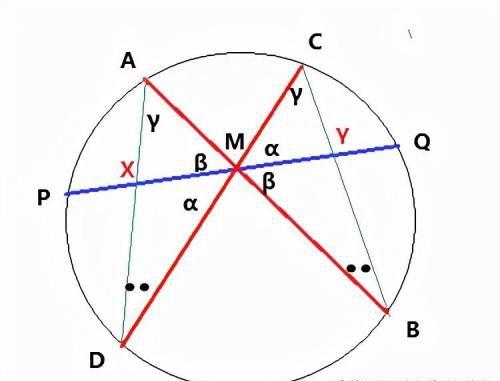
AX·XD= PX·XQ

= a² - x².

在三角形DXM中，根据正弦定理：

DX= x·sin(α)/sin(180° - (α + β + γ))

= x·sin(α)/sin(α + β + γ).

在三角形AXM中：

AX = x·sin(β)/sin(γ),

将上面两个等式相乘：

AX·DX = x²·sin(α)·sin(β)/sin(γ)·sin(α + β + γ) = a² - x².

根据此等式可得出：

x² = a²·sin(γ)·sin(α + β + γ))/(sin(α)·sin(β) + sin(γ)·sin(α + β + γ)).

可以看到等式的右侧对于α和β是对称的，如果对于y=MY做同样的运算，我们会得到与右侧相同的等式，所以

x=y

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小思创作整理编辑！