导语：矩形折叠模型（中考必备）

折叠动点问题是中考的难点和重点，形式多种多样，下面给出几道以矩形为模型的折叠问题，熟悉以下模型，对其它类型的折叠问题也有帮助。

1、矩形沿对角线折叠模型

如图，矩形ABCD沿着对角线BD折叠，使点C落在E处，BE交AD于点F，若AD=8,AB=4，则DF的长为_______。

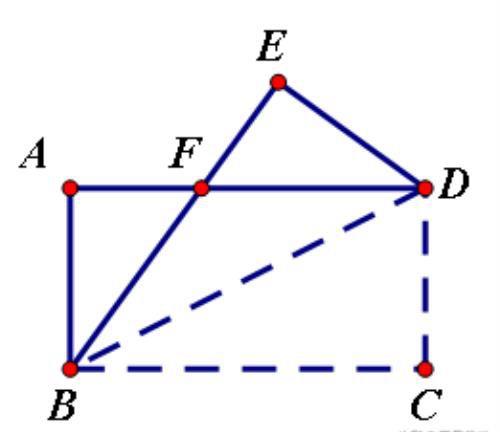
分析：阴影两个三角形全等，设DF=x,利用△DEF建立勾股定理可求DF.

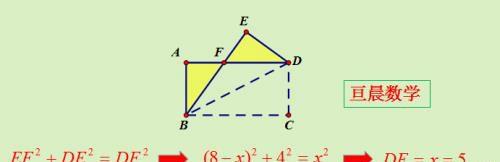
2、矩形折叠顶点至边模型

如图，E是矩形ABCD边AB上的点，将矩形ABCD沿DE折叠，使得点A落在边BC上，若AD=5,AB=4，求AE的长。

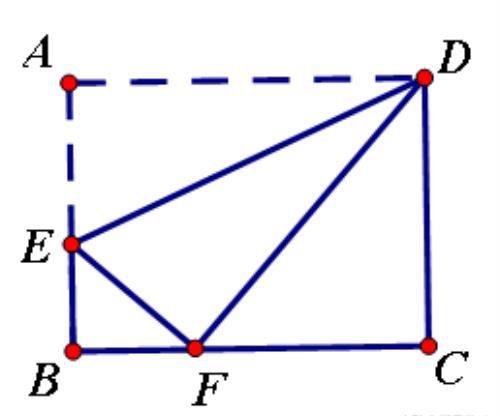
分析：设AE=x,利用△BEF建立勾股定理可求AE.

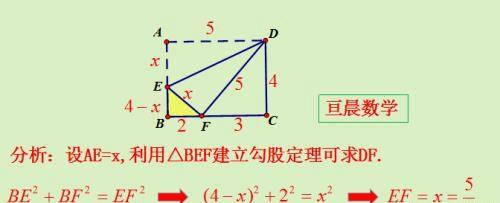
3、矩形折叠顶点至对角线模型

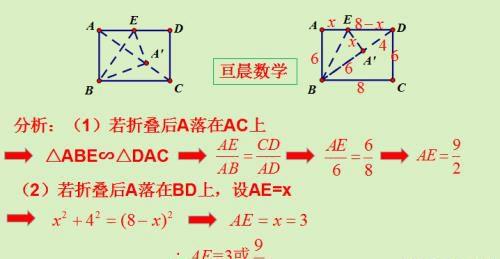
如图，已知矩形ABCD，AB=6,BC=8，E是AD边上一动点，沿BE折叠矩形ABCD使得顶点A落在矩形ABCD的对角线上。则AE=_______.

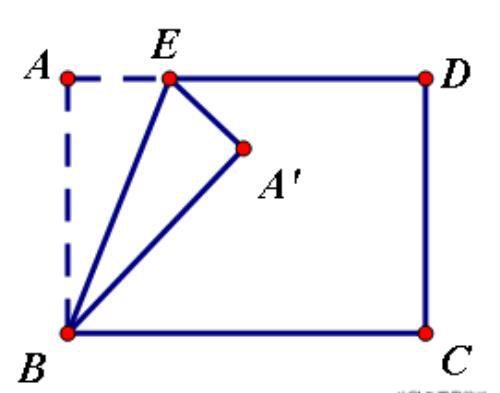
分析：矩形对角线有两条，需要分两种情况讨论。

4、折叠顶点至边中垂线线模型

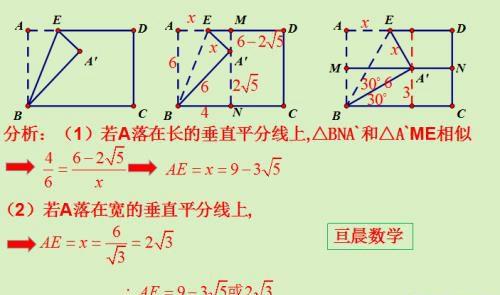
如图，已知矩形ABCD，AB=6,BC=8，E是AD边上一动点，沿BE折叠矩形ABCD使得顶点A落在矩形ABCD的边的垂直平分线上。则AE=_______.

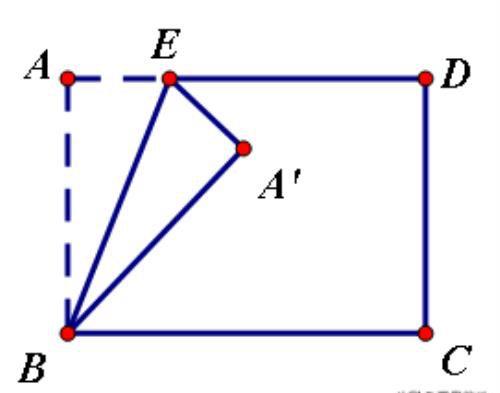
分析：矩形边中垂线有两条，需要分两种情况讨论。

5、矩形对角折叠模型

如图，E和F是矩形ABCD边AD、BC上的点，将矩形ABCD沿EF折叠，使得点A与点C重合，若AD=8,AB=4，求折痕EF的长。

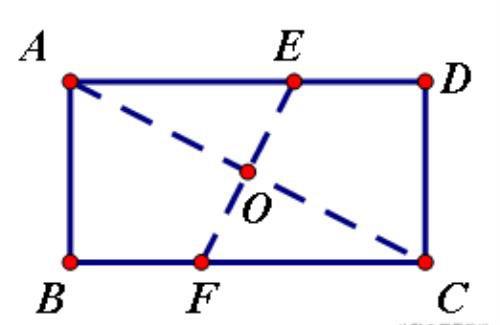
分析：其实折痕EF和对角线AC互相垂直平分

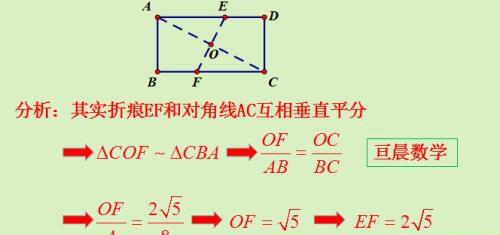
总结此题折痕公式：

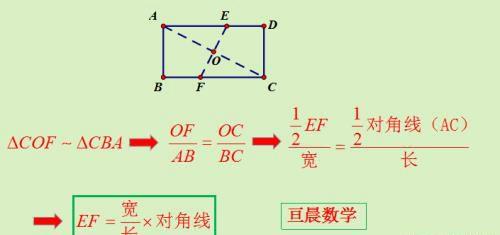
6、矩形折叠共线模型

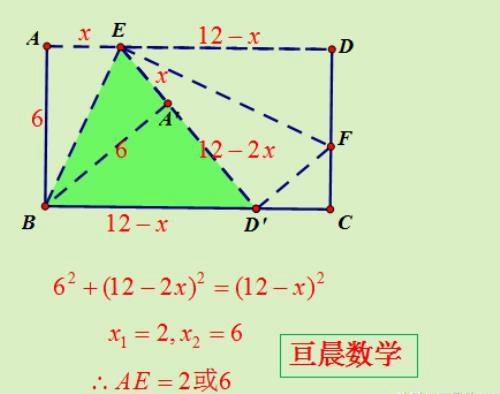
如图，已知一个矩形纸片ABCD，AB=6，BC=12，点E为AD边上的动点（点E不与点A，D重合），经过点A,E折叠该纸片，得点A′和折痕BE，经过点E再次折叠纸片，使点D落在直线EA′上，得点D′和折痕EF。当点D′恰好落在边BC上时，AE的长为 。

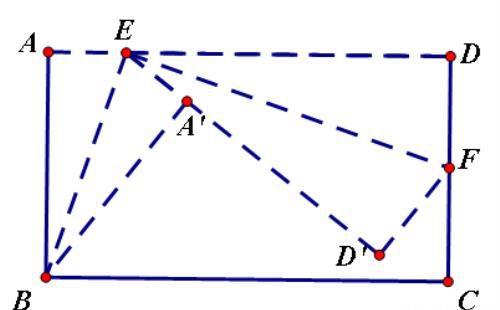
分析：本题要先证明三角形BED′是等腰三角形，即D′E=D′B；而后利用三角形A′D′B是直角三角形建立方程。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小德创作整理编辑！