> 动物

等积式和比例式的区别(等比例求积公式)

导语：等积式和等比式-△应用4:三者比

如果x＝y，那么x︰y＝︰＝3︰10。

其实，x＝y可以化成x＝y(与分子化相同)，这时候与x相乘的分数分母为3，与y相乘的分数分母为10，所以x︰y＝3︰10。

上面求比的方法称为“分子化同”法，这一方法主要适用于多个字母的比。

例　如下图，长度和是360厘米的A、B、C三根木棒插在水池中，A棒有露出水面，B棒有露出水面，C棒有露出水面。水池有多深？

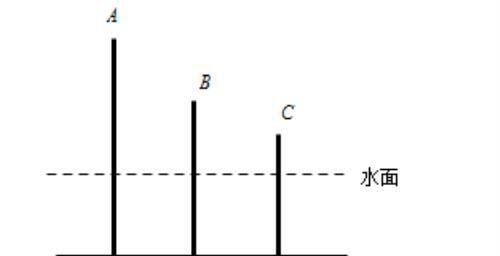
解析

(1) 每根小棒在水中部分一样长，即

×A长＝×B长＝×C长

A长＝B长＝C长

分子化同：A长＝B长＝C长

A长︰B长︰C长＝12︰7︰5

(2) 三根小棒长共24份，共360厘米，1份＝15厘米，

A小棒长＝12×15＝180(厘米)

A小棒在水中部分长(即水池水深)＝180×＝45(厘米)

(3) 分子化同后所得的比，用于看份数时，一定不要化简。

答案

12＋7＋5＝24

360÷24＝15(厘米)

12×15×

＝3×15

＝45(厘米)

答：水池深45厘米。

练习

1. 如下图，长度和是260厘米的A、B、C三根木棒插在水池中，A棒有露出水面，B棒有露出水面，C棒有露出水面。水池深多少厘米？

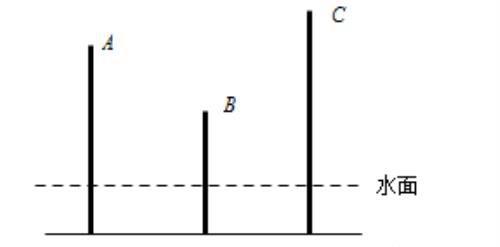
2. 育才小学四、五、六年级的学生共植树450棵，已知四年级已经植完了自己任务的，五年级已经植完了自己任务的，六年级已经植完了自己任务的，并且他们剩下的棵数相同。一共还剩多少棵没有植？

解析

(1) 每根小棒在水中部分一样长，即

×A长＝×B长＝×C长

A长＝B长＝C长

分子化同：A长＝B长＝C长

A长︰B长︰C长＝24︰14︰27

(2) 三根小棒长共65份，共260厘米，1份＝4厘米，

A小棒在水中部分长为6份(分子化同后的分子)，

A小棒在水中部分长(即水池水深)＝6×4＝24(厘米)

答案

260÷(24＋14＋27)＝260÷65＝4(厘米)

6×4＝24(厘米)

答：水池深24厘米。

解析

(1) 四年级完成任务的，余

五年级完成任务的，余

六年级完成任务的，余

三个年级剩下的棵数相同，得：

四年级棵数＝五年级棵数＝六年级棵数

分子化同，得：

四年级棵数＝五年级棵数＝六年级棵数

三个年级的棵数比是：

四年级棵数︰五年级棵数︰六年级棵数

＝12︰15︰18 …不化简

(2) 共45份，共450棵，1份＝10棵，

四年级剩下棵数＝10×10＝100(棵)　…剩下10份，1份10棵

共剩棵数＝100×3＝300(棵)

答案

450÷(12＋15＋18)＝450÷45＝10(棵)

10×10＝100(棵)

100×3＝300(棵)

答：一共还剩300棵没有植。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小竹创作整理编辑！