梯形面积公式与等差数列原理(梯形面积等比公式)

导语：小学数学难点——梯形面积公式和等差数列求和啥关系？

学习“梯形的面积”，有这样一道习题:“我们经常见到圆木、钢管等堆成像下图的形状,请计算图中的总根数。”

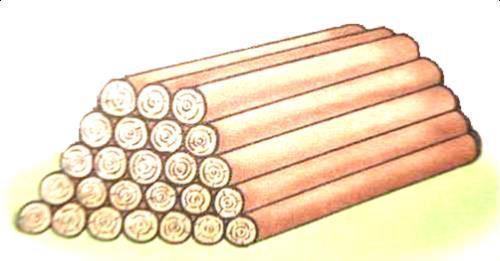
观点1、这堆圆木的“横截面像个梯形”,“上层根数相当于梯形的上底,下层根数相当于梯形的下底,层数相当于梯形的高”,而“梯形面积=（上底+下底）×高÷2”,所以,“圆木的总根数=（上层根数+下层根数）×层数÷2”。所以求圆木总根数,就是应用梯形面积计算公式。

观点2、这道题目的要求是求圆木的总根数,而不是求那个“横截面”的面积，怎么能用梯形面积公式去计算呢？如果仔细看，这个截面并不是一个标准的梯形啊,它的边线不是直的线段，而是一些弯的弧线。另外，圆木并没有填满整个梯形的“面”，圆木之间有空隙呀！

咋办呢？

为了增加理解，先写出来吧（方法是不是太笨了，哈！为了建立概念）

3+4+5+6+7+8，怎样求它们的和呢？有巧算的办法吗？我们可以用3+8=11,4+7=11,5+6=11,

再用11×3=33（根），这是那个叫做高斯的小朋友解决问题的办法，如果把这一列数字倒着写过来，8+7+6+5+4+3，相对应的两个数字的和都相等，用（3+8）×6=66，也就是用（最上层根数+最下层根数）×层数，就算出了两列数字的和，再除以2就是一列数字的和了。想一想，这种算法跟梯形面积的计算方法有联系吗？

其实在研究梯形面积的计算方法时，是用两个完全一样的梯形拼成了一个平行四边形，用转化的方法来计算梯形的面积，如果再有同样的一堆木头，如果能倒放在旁边，也就能组成了一个平行四边形，这样每层的根数就一样多了，每层的根数就是3+8=11根，用11×6=66（根）就算出了两堆这样的木头的数量，然后除以2就是一堆的数量了。

求总根数公式可以写成：总根数=（上层根数＋下层根数）×层数÷2,表面上看它确实很像梯形面积计算公式：梯形面积=（上底+下底）×高÷2。但实质上并不是。我们可以把它作为有趣的数字和图形结合来记忆呢。也就是求等差数列3、4、5、…8的和的问题。

计算公式应是：和=（首项+末项）×项数÷2，参考一下上篇文章哦

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小萱创作整理编辑！