求面积的方法(求面积的两种方法)

导语：求面积这种方法太简单了，一学就会——等量代换求面积

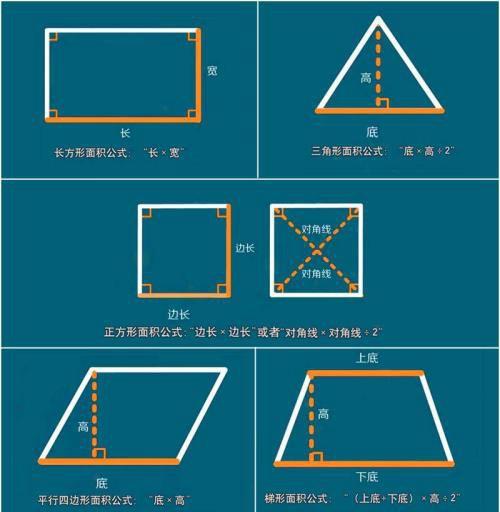
先回顾一下各图形面积公式：

要熟练应用以上公式

以上公式都是最基础的，但还是远远不够用的，还需要掌握一些特定的性质和技巧来解决面积的问题。接下来我们就来学习面积求解技巧中的等量代换法。

这两个性质对图形问题上帮助特别大！

比如下面这道例1题:

题中阴影部分的梯形无法直接求出来，这时可以用等量代换的方法求出来。那就要在图中找到与阴影部分相同的图形，如下图图一所示，蓝色部分为面积相等的两个部分。

图一

接下来把图形用①②③做标记如图二所示

图二

两个大三角形减去公共的图形②如下图三所示：

图三

因为两个大三角形面积相等，所以①与③面积相等。

解题思路：面积①＋面积②＝面积③＋面积②

面积①＝面积③（这样就可以通过求图形①的面积来求阴影的面积）

图四

上图四红色线段为两个大三角形的公共边，去掉红色公共边，两边的线段是相等的，都是8。这样我们要求的直角梯形图形①的高就是8。再用大三角形的高14减去多出来的5，得到直角梯形的上底是9，如下图五所示。

图五

直角梯形的上底为14-5＝9（厘米）

根据梯形面积公式＝（上底 ＋下底）×高÷2得到

＝（9＋14）×8÷2

＝92（平方厘米）

答：阴影部分的面积是92平方厘米。

本题就是通过等量代换的思想，不直接求阴影面积。

例2题：

图一

图二

图三

图四

以上两道题都是直接在题目中寻找和阴影部分相同的部分，思路比较简单。下节内容提示：等量代换另一种题型----求面积差。想学习更多题型，点关注，点红心，更多精彩内容持续更新。

本文内容由小竹整理编辑！