命题及其关系充要条件教案(命题和充要条件)

导语：3、命题及其关系、充要条件

1、命题

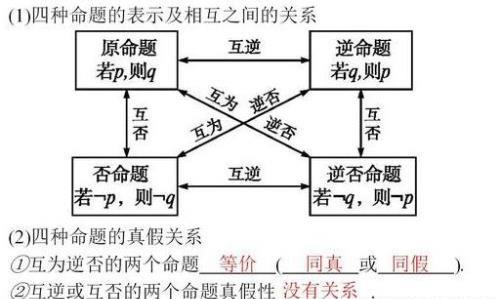
2、四种命题及其关系

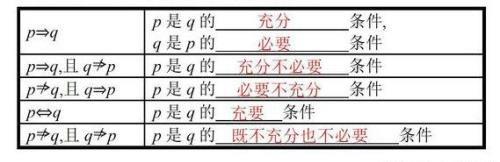
3、充分条件、必要条件与充要条件的概念

常用结论

考点自测

命题及其相互关系

思考由原命题写出其他三种命题应注意什么?如何判断命题的真假?

解题心得1

写一个命题的其他三种命题时,需注意:

(1)对于不是“若p,则q”形式的命题,需先改写;

(2)若命题有大前提,则写其他三种命题时需保留大前提.

2.判断一个命题为真命题,要给出推理证明;判断一个命题为假命题,只需举出反例即可.

3.根据“原命题与逆否命题同真同假,逆命题与否命题同真同假”这一性质,当一个命题直接判断不易进行时,可转化为判断其等价命题的真假.

充分条件、必要条件的判断（多考向）

解题心得充要条件的三种判断方法:

(1)定义法:根据p⇒q,q⇒p是否成立进行判断.

(2)集合法:根据p,q成立对应的集合之间的包含关系进行判断.

(3)等价转化法:一是指对所给题目的条件进行一系列的等价转化,直到转化成容易判断充要条件为止;二是指根据一个命题与其逆否命题的等价性,把判断的命题转化为其逆否命题进行判断.

充分条件、必要条件的应用

思考如何求与充要条件有关的参数问题?如何证明一个命题是另一个命题的充要条件?

解题心得

1.与充要条件有关的参数问题的求解方法:解决此类问题一般是根据条件把问题转化为集合之间的关系,并由此列出关于参数的不等式(组)求解.

2.充要条件的证明方法:在解答题中证明一个命题是另一个命题的充要条件时,其基本方法是分“充分性”和“必要性”两个方面进行证明.

要点归纳总结

易错点警示

1.当一个命题中含有大前提时,其他三种命题也必须含有该大前提,也就是大前提不变.

2.在判断命题的真假及写四种命题时,一定要明确命题的结构,可以先把命题改写成“若p,则q”的形式.

3.判断条件之间的关系,要注意条件之间的推出方向,正确理解“p的一个充分不必要条件是q”等语言.

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小纳创作整理编辑！