高中函数应用题的求解策略(高中数学函数常用方法)

导语：广泛应用的必备技能，求解高中数学“函数单调性”问题方法与技巧

1. 基本问题说明

一般地，已知某函数模型，分析、判定其单调性；反过来，根据得到的函数单调性，转化为相关代数关系(等式或不等式)，以求解待求问题，如最值、值域、参数值范围等。

这是一类很常见的基础应用，既可以单独作为选择题或填空题，也可以广泛地综合到求解析式、值域或最值问题、恒成立问题、存在性问题、参数问题、解不等式等题型中。

2. 解决问题的一般方法

1) 单调性判定

① 直接法

多见于简单的常见初等函数相关题型，直接根据性质或图像特征进行判定；

② 定义法

第一定义(即课本的定义)：“设值、作差、定号”，这是未学导数前一般方法；

第二定义：设函数f(x)的定义域为D，在定义域内任取x1、x2，且x1≠x2，若(f(x1)-f(x2))/(x1-x2)>0，则函数单调递增；若有(f(x1)-f(x2))/(x1-x2)<0，则函数单调递减。

③ 导数法(先知道有这么一个非常好用方法，等学过选修2-2的导数部分后再回来融会贯通)

“求导数、求零点、（按需分段）判单调” ，这是学过导数后的一般方法。

导数与函数单调性密切相关。它是研究函数的另一种方法，为其开辟了许多新途径。特别是对于具体函数，利用导数求解函数单调性，思路清晰，步骤明确，既快捷又易于掌握；利用导数求解函数单调性，要求熟练掌握基本求导公式。

思考：对比导数法的定义与判定单调性的定义法，试分析二者之间的区别与联系。

对于复合函数，可以先分别判断每一级函数的单调性，然后再分析、判断把它们复合在一起后的单调性，如两级函数复合在一起的单调性一般可利用“同增异减”性质来判定（单调区间的定义域要一致）。

2) 单调性逆用

根据已知的或构造的函数的单调性，转化得到所需代数关系如等式、不等式等后，即可求解待求问题，如最值、值域、参数值范围等。其求解过程的要领有：

① 按需多画图，有助于分析、思考和减少失误；

② 不要忘了分析或考虑单调区间的非极值点端点。

3.典型示例

例1 证明函数f(x) = 3x+2在R上是增函数。

证明：设x1,x2是R上任意实数，且x1<x2即x1-x2<0，(提示：设值)

则f(x1)-f(x2)=3x1+2 – 3x2-2 (提示：作差)

=3(x1-x2)<0 (提示：定号)

所以函数f(x) = 3x+2在R上是增函数。

讲解：

① 判定单调性一般方法（必须记住 – “设值、作差、定号”）

依次为：设值 -> 作差 -> 判定符号 –> 得出结论（增、减或不定）。

② 判定符号时，若无法直接得出结果，可通过分析法或分类讨论来判定符号性质。

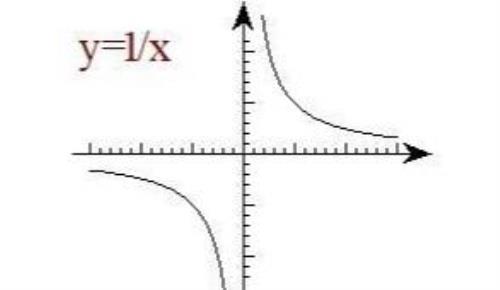
例2 求出函数f(x)=1/x的单调区间。

解：（直接法）由反比例函数性质可知，

f(x)单调区间为(-∞,0)、(0,+∞)，且都为单调递减区间。

讲解：

① 思考：函数f(x)=1/x是减函数吗？不是，比如-1<1但f(-1)<f(1)。这是一个易错点！如图， 一目了然。

② 当有多个单调区间时，需检查和分析相邻单调区间的边界处是否满足单调递增或递减，若满足，则单调区间可“并”在一起；否则只能“和”在一起。

例3 判断f(x)=2x^3+3x^2-12x+1的单调性，并求出单调区间。

解：（高次函数一般用导数法）

因为f(x)= 2x^3+3x^2-12x+1，

所以f'(x)=6x^2+6x-12

当f'(x)>0时，即x>1或x<-2时，

函数为f(x)为单调递增；

当f'(x)<0，即-2<x<1时，

函数f(x)为单调递减。

如图：

例4 求函数y=（4x+3）/(x^2+1)的值域。

解：（单调性在求值域中应用）依题意，

讲解：

① 单调性基础应用广泛地出现在求解析式、值域或最值问题、恒成立问题、存在性问题、参数问题、解不等式等题型中，这里就不再一一举例了，详见有关题型的典型例题。大家只需记住，这类问题中，单调性一般是主要的、便捷的解题方法之一。

② 提示：本题的函数在±∞出无限趋近于0,所以在两个极值点处分别取得最大值和最小值，如图。

但是，有时端点处的值可能比极大值大或比极小值小。所以，求最值时不要忘了把非极值点端点考虑进来！

例5 已知函数f(x)=4x^2-kx-8在区间[5，20]上有单调性，求参数k的取值范围。

解：（单调性的逆用）依题意，

因为f(x)=4x^2-kx-8的对称轴为x=k/8，

开口向上，所以在对称轴右边递增，左边递减；

又因为函数f(x)=4x^2-kx-8在区间[5，20]上有单调性，

所以k/8 ≥ 20 或k/8 ≤ 5,

解得：k≥160或k≤40

所以所求参数k的取值范围是： k≤40或k≥160。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小楠创作整理编辑！