等腰三角形三线合一可以得到什么(等腰三角形三线合一是哪三线)

导语：等腰三角形三线合一，这条线上任意点，到底角顶点距离相等

初中数学，等腰三角形中一个关键的知识点就是，等腰三角形顶角的角平分线，底边的高，中线三线合一，利用好这一特性，可以帮我们快速解答很多问题，因此，灵活应用这一知识点，就是我们今天要分享的内容。

例题一：如图，在△ABC中，AB=AC，△ADE的顶点D、E分别在BC，AC上，且∠DAE=90°，AD=AE,若∠C+∠BAC=145°，则∠EDC的度数为（）

A 17.5° B 12.5° C 12° D 10°

解析：∵∠C+∠BAC=145°，由三角形内角和定理，可以得出

∠B=35°

∵AB=AC,由等腰三角形性质，可以得出

∠B=∠C=35°

又∵△ADE是等腰直角三角形

∴∠ADE=∠AED=45°

又由三角形外角定理，可以得出

∠AED=∠CDE+∠C

∴∠CDE=10°，答案选D

例题二：如图所示，已知△为直角三角形，∠B=90°，若沿图中虚线剪去∠B，则∠1+∠2等于（）

A 90° B 135° C 270° D 315°

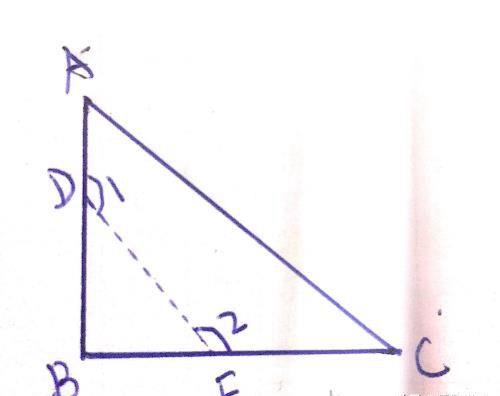
由三角形外角定理，可以得出

∠1=∠B+∠BED

∠2=∠B+∠BDE

由直角三角形两个锐角和等于90°，可以得出

∠BDE+∠BED=90°

∴∠1+∠2=3∠B=270° 且∠1+∠2=3（∠BAC+∠BCA）

小结：将直角三角形的直角剪去后，会得到两个新的角，那这两角的和，等于直角的3倍，等于原直角三角形两个锐角和的3倍，等于270°。

例题三：在△ABC中，AD平分∠BAC,BD⊥AD，垂足为D，过D作DE//AC,交AB于E，若AB=5，求线段DE的长。

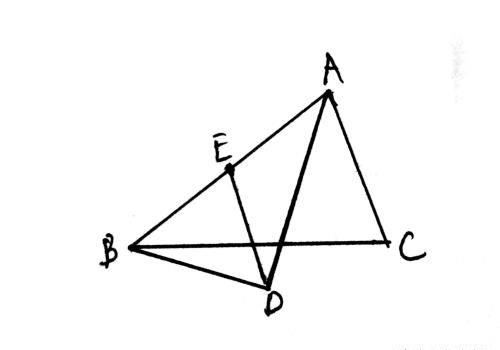
解析：∵DE//AC,由平行线同位角相等定理，可以得出

∠BAC=∠BED

由∵AD是∠BAC的角平分线

∴∠BAD=1/2∠BAC

由三角形外角定理，可以得出

∠ BED=∠BAD+∠EDA

∴∠BAD=∠EDA，ED=EA

由直角三角形两锐角和等于90°，可以得出

∠EBD+∠EAD=90°

且∠BDE+∠EDA=90°

∴∠EBD=∠BDE，ED=EB

∴DE=EB=EA=1/2AB=5/2

关于等腰三角形的一些知识点，今天就为大家分享到这里，希望这些内容对大家有帮助。如果觉的有用就给个关注，多多转发，收藏，谢谢大家。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小信创作整理编辑！