初中几何辅助线难题(初中几何辅助线大全及口诀)

导语：中考几何进阶 辅助线法则（17）几何最值：阿氏圆的性质和应用

中考几何进阶 辅助线法则（17）几何最值：阿氏圆的性质和应用

阿氏圆

在胡不归模型末尾的引申思考里，我们提出了这样的问题：

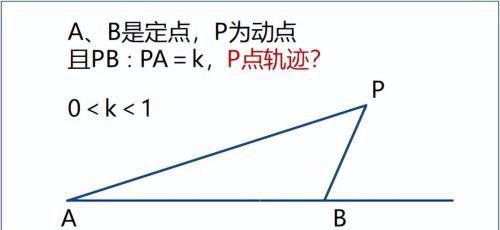
知识储备足以支撑“独立研究”这个问题。

没有思路，就从探讨特殊位置开始。

1）当P落在线段AB之间记为M。

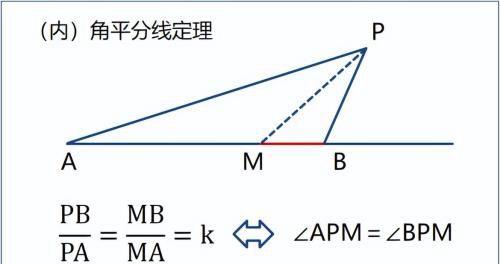
则有：MB∶MA＝k，即：

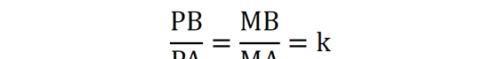
这恰好是三角形（内）角平分线定理。PM平分∠APB；此外，因为A、B均是定点，所以M也是定点。

2）当P落在AB延长线上记为N。

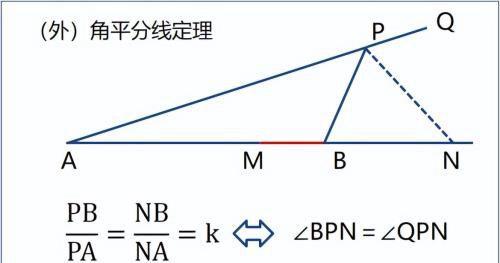
则有：NB∶NA＝k，即

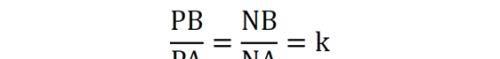
这正是三角形外角平分线定理。同样地，N是定点。

3）P点轨迹

把两张分析图结合。内角平分线与其外角平分线互相垂直，所以，P对固定线段MN所张的角 始终是直角：∠MPN＝90°。

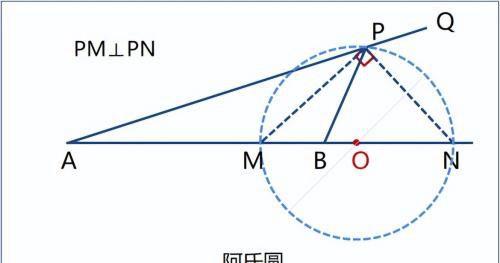
由是，P点的轨迹是一个圆，圆心O是MN的中点。这个圆就叫做“阿氏圆”。P、A、B、M、N、O是阿氏圆的重要关联点。其中P是动点，其它均为定点。

阿氏圆性质

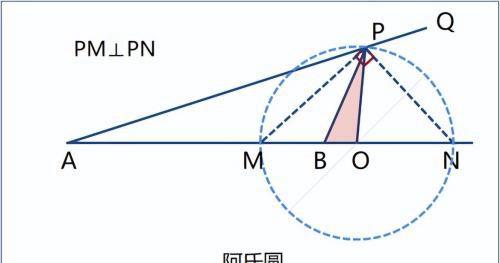
1）PM平分∠APB，PN平分∠NPQ，关联线段比：

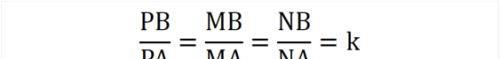
2) △OPB∽△OAP，事实上：

或者

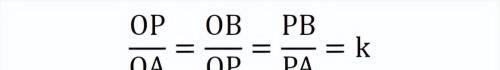
证明：

两个三角形有一个共用角∠POB＝∠AOP，所以若构成该共用角的两边对应成比例，则这俩三角形相似。设圆半径为r，则

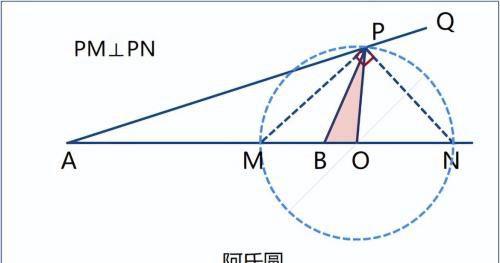
MA＝OA－OM＝OA－r；

MB＝OM－OB＝r－OB；

NA＝OA＋ON＝OA＋r；

NB＝OB＋ON＝OB＋r；

由1）MB∶MA＝NB∶NA得：

整理得：

注意到OP＝r，代入上式，即有：

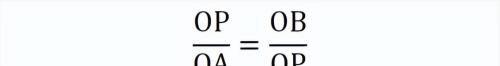
由此△OPB∽△OAP（SAS），且

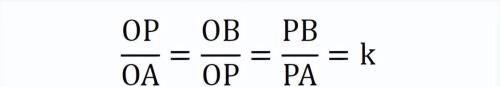
阿氏圆模型

求PB＋k·PA，0＜k＜1，的最小值。

首先需要说明的是，阿氏圆模型适用范围很窄。这类问题的设计是被严格制约的。

A是定点。一旦圆心的位置O也确定了，那么动点P必须限制在以O为圆心，以r＝k·AO为半径的圆上，min[λ(PB＋k·PA)]，0＜k＜1,λ＞0，k、λ是常系数，才可以阿氏圆模型求解。

〖分析〗

和胡不归模型的思路相近，想办法把PB＋k·PA中的k·PA转换为线段PC，即找到线段PC＝k·PA。这样，求PB＋k·PA的最小值，就转换为求PB＋PC的最小值。而PC∶PA＝k，因此这种转换就牵连到阿氏圆中的线段比的性质。

1）注意区分定点A和B：A是系数小于1的线段的定点；

2）C在OA上，且OC＝k· OP；连接PC，则△OPC∽△OPA，PC＝k· PA。A、C、M、N、O就是圆⊙的阿氏圆关联点（均为定点）。

3）连接BC，在△BCP中，PB＋PC≥BC，仅当P落在BC上，取得最小值BC：即min(PB＋k· PA)＝min(PB＋PC)＝BC。

经典题例

例题 Rt△ABC中，∠C＝90°，AC＝4，BC＝3，圆C半径为2，分别交AC、BC于D、E。P是圆C上动点，

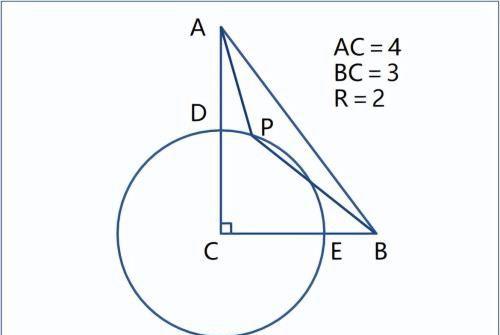
求：① 设PA/2＋PB最小值；② PA＋2PB最小值；③ PA＋2PB/3最小值；④ 3PA/2＋PB最小值。

〖分析〗

① PA/2＋PB最小值；

记k＝1/2。∵CP∶CA＝1∶2，∴若k≠1/2，则k·PA＋PB不能用阿氏圆模型求解。

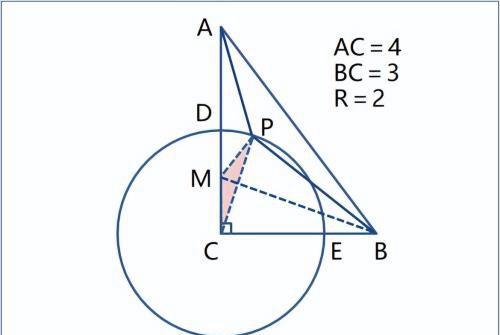
1）系数小于1 的线段的定点是A点；

2）在AC上取点M，使得CM＝k·CP＝CP/2＝CD/2，也就是取CD的中点M。连接PC、PM，则PM＝k·PA＝PA/2

3）连接BM，在△PBM中：PM＋PB≥BM，即PA/2＋PB≥BM，仅当P在BM连线上，取得最小值BM。

在Rt△BCM中，计算得BM＝√10。

② PA＋2PB最小值；

PA＋2PB＝2（PA/2＋PB）；故 min(PA＋2PB) ＝2 min(PA/2＋PB)＝2√10。

③ PA＋2PB/3最小值；

记k＝2/3。同理，∵CP∶CB＝2∶3，∴若k≠2/3，则k·PB＋PA不能用阿氏圆模型求解。

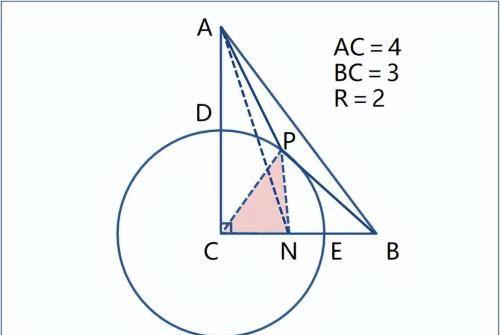
1）系数小于1的线段的定点是B点；

2）在BC上取一点N，使得CN＝k·CP＝2CP/3＝2CE/3，连接PC、PN，则PN＝k·PB＝2PB/3

3）连接AN，在△PAN中：PA＋PN≥AN，即PA＋2PB/3≥AN，仅当P在AN连线上，取得最小值AN。

在△CAN中，计算得AN＝4(√10)/3。

④ 3PA/2＋PB最小值；

3PA/2＋PB＝3/2（PA＋2PB/3）；故 min(3PA/2＋PB) ＝3/2 min(PA＋2PB/3)＝2√10。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小鸣创作整理编辑！