旋转值之瓜豆原理(瓜豆原理怎么找从动点圆心)

导语：旋转法、构造法、瓜豆原理：处理线段最值

方法一：旋转法（旋转其目的是转化线段最值）如图

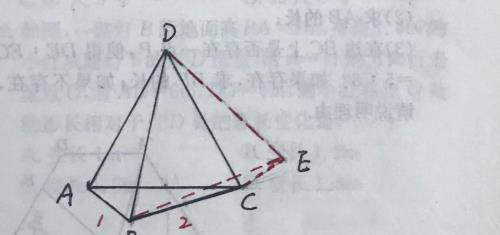
分析：将△ABD绕点D逆时针旋转60°得到△CED

∴CE=AB=1，

易证：△BDE为等边三角形

∴BE=BD

即：BD最值转化为求BE最值

如图BC-CE≤BE≤BC+CE

∴1≤BE≤3

即：BD最大值为=3，最小值=1 。

方法二：构造手拉手模型

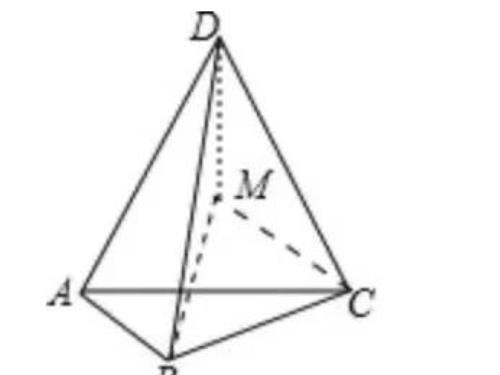
分析：如图以BC为边作等边△BCM，连接DM

∴BM=BC=2

手拉手模型易证：△DMC≌△ABC

∴DM=AB=1

如图BM-DM≤BD≤BM+DM

∴1≤BD≤3

即：BD最大值为=3，最小值=1 。

方法三：瓜豆原理

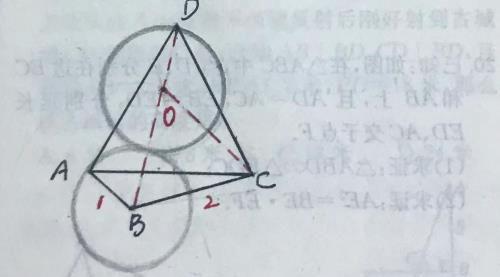
分析：不妨把B、C看作不动点，点A看作动点

分析：主动点：A，从动点：D，中心点：C

主动点A运动轨迹：是以点B为圆心，以AB长为半径的⊙B上运动。

从动点D:是主动点A，以点C为旋转中心顺时针旋转60°得到。

∴从动点D：是主动点A对应轨迹顺时针旋转60°得到。

将CB绕点C顺时针旋转60°得到CO（圆心也顺时针旋转60°）

∴点D运动轨迹：以O为圆心，OD长为半径的⊙O上运动

∴OD=AB=1

易证：△OBC为等边三角形

∴OB=BC=2

如图OB-OD≤BD≤OB+OD

∴1≤BD≤3

即：BD最大值为=3，最小值=1 。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小婷创作整理编辑！