微分方程及其通解与特解(如何由微分方程的通解求出微分方程的特解)

导语：微分方程的基本概念（微分方程的通解与特解）

微分方程： 一阶微分方程、二阶微分方程、三阶微分方程……

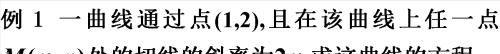
斜率y&39;,…y^<n>)=0

这里x为自变量，y是x的未知函数，而y,…y^(n)依次是y的一阶、二阶，……，n阶导数。

例1: 求微分方程dy/dx=3x^2的通解，并求满足初值条件y|x=2=1的特解。

解：直接积分得方程的通解为：y=x^3+C

代入初值条件：当x=2，y=1解得C=-7

满足初值条件的特解为y=x^3-7

例2： 验证：函数x=C1coskt+C2sinkt是微分方程d^2x/dt^2+k^2x=0的解.并满足初始条件x|t=0=A,dx/dt|t=0=0的特解.并求满足初始条件x|t=0=0的特解.

解：因为dx/dt=-kC1sinkt+kC2coskt,d^2/dt^2=-k^2C1coskt

-k^2C2sinkt=-k^2x,

函数x=C1coskt+C2sinkt有两个任意常数，且是方程的解。故是方程的通解.

代入初值条件：x|t=0=A,dx/dt|t=0=0

C1=A,C2=0,代入函数x的表达式中，得到特解:x=Acoskt

小结：微分方程非初值问题（即无初始条件）的解是通解，其几何图形是曲线族；微分方程初值问题的解是特解，其图形是一条曲线.反过来，微分方程反映了满足此方程的曲线（族）的特征.

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小涵创作整理编辑！