圆锥曲线中的热点问题(漫谈圆锥曲线)

导语：它是圆锥曲线的热点内容，好好学习，必能提升成绩

抛物线是一类运用广泛的圆锥曲线，由动点、焦点、离心率和准线构成和谐的整体，是高考中常考常新的热点问题，那么高考常以何种方式考查抛物线的哪些内容？

抛物线是高中数学的重要内容之一，同时也是高考重点考查的内容，抛物线的概念和性质，直线与抛物线的位置关系等知识既是高考关注之处，又是学生学习中易出错的地方。

高考对抛物线的考查基本围绕定义的应用以及几何性质，命题方向上注重，侧重基本运算能力和思维的灵活性，而与抛物线有关的最值问题是高考中的常见问题。

抛物线有关的高考试题分析，典型例题1：

已知圆C过抛物线y²=4x的焦点，且圆心在此抛物线的准线上，若圆C的圆心不在x轴上，且与直线x+√3y﹣3=0相切，则圆C的半径为　 　．

考点分析：

抛物线的简单性质．

题干分析：

求出抛物线的准线方程x=﹣1，设圆心坐标（﹣1，h），根据切线的性质列方程解出h，从而可求得圆的半径．

抛物线有关的高考试题分析，典型例题2：

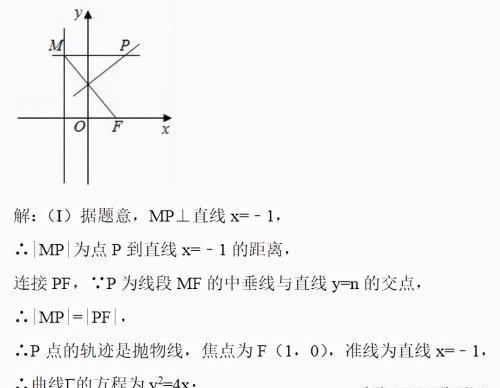
在平面直角坐标系xOy中，点F（1，0），直线x=﹣1与动直线y=n的交点为M，线段MF的中垂线与动直线y=n的交点为P．

（Ⅰ）求点P的轨迹Г的方程；

（Ⅱ）过动点M作曲线Г的两条切线，切点分别为A，B，求证：∠AMB的大小为定值．

考点分析：

抛物线的简单性质．

题干分析：

（Ⅰ）连接PF，运用中垂线的性质可得|MP|=|PF|，再由抛物线的定义可得点P的轨迹方程；

（Ⅱ）求得M（﹣1，n），过点M的切线斜率存在，设为k，则切线方程为：y﹣n=k（x+1），联立抛物线的方程，消去y，运用相切的条件：判别式为0，再由韦达定理，结合两直线垂直的条件：斜率之积为﹣1，即可得证。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小冰创作整理编辑！