数学高中难题巧解例题(数学题高中难题)

导语：一道高中数学难题的解法对比

一道高中数学的线段最值问题

【题目】如图，平面四边形ABCD的对角线交点位于四边形的内部，AB=1，BC=√2，AC=CD，AC⊥CD，当∠ABC变化时，对角线BD的最大值为 ．

分析：

①已知四边形中部分的边长关系求另外的边，容易想到的就是解三角形，因此考虑用正弦定理与余弦定理；

②由于求最值，又容易想到用导数的方式去解决；

③因为原题是高中数学题，所以思维定势，一般只能想到上面的两种方法，但是其实用初中几何辅助线的方式可以快速解决．见等腰则考虑使用旋转．

答案：

【方法一】（三角函数法）：

解：设∠ABC＝α，∠ACB＝β，

由余弦定理可得

AC²=1+2-2√2cosα＝3﹣2√2cosα，

∴AC=√(3-2√2 cosα)=CD．

由正弦定理可得：

sinβ=(√2sinα)/√(3-2√2 cosα)，

∴BD²＝2+3﹣2√2cosα﹣2×√2×√(3-2√2 cosα)cos（90°+β）

＝5﹣2√2cosα+2√2×√(3-2√2cosα)sinβ

＝5﹣2√2cosα+2√2sinα

＝5+4sin(α-π/4)，

∴α=3π/4时，BD²有最大值9，

即BD的最大值为3．

【方法二】（导数法）：

解：设∠ACB＝α，

AC=t（√2-1＜t＜√2+1），

由余弦定理可得

cosα=（t²+2-1）/2√2t，

∴sinα=√（1-cos²α）

=√[-（t²-3）²+8]/2√2t，

在△BCD中，由余弦定理得，

BD²=BC²+CD²-2BC·CDcos∠BCD

=2+t²+√[-（t²-3）²+8]，

设t²-3=x（-2√2＜x＜2√2），

则BD²=5+x+√（8-x²），

设f（x）=5+x+√（8-x²），

则f′（x）=1+2x/（8-x²）

=-（x²+2x-8）/8-x²，

当x=-2时，f′（x）=0，

当-2√2＜x＜-2时f′（x）＜0，f（x）单调递减，

当-2＜x＜2√2时f′（x）＞0，f（x）单调递增，

∴当x=2时，BD²的最大值为f（2）=9，即BD的最大值为3．

【方法三】（旋转法）：

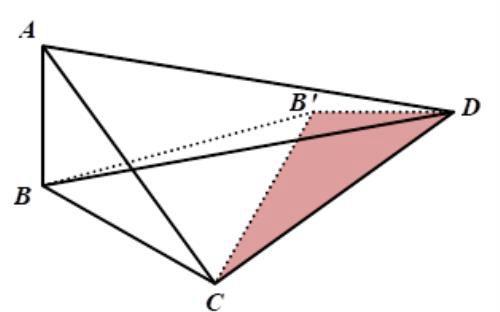
解：如图，将△ABC绕点C逆时针旋转90°，

使得AC与DC重合，点B落在点B′上，

∴△BCB′为等腰直角三角形，BB′=2，B′D=AB=1，

∵BD≤BB′+B′D=2+1，

∴BD的最大值为3．

【总结】

观察下面的动图，我们可以发现点C是以B为圆心，√2为半径的圆上运动的，当B、B′、D三点共线的时候分别取到最大值和最小值，也就是

2-1≤BD≤2+1．

很多时候题目的难易就在一个点上，如果突破了，那么就不难了．阻碍我们的常常就是那个“思维定势”．

往期精选：

旋转

图形变换求几何最值

常见几何最值问题模型归纳

两道线段最值问题解析

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小珊创作整理编辑！