导语：大数据：如何用决策树解决分类问题

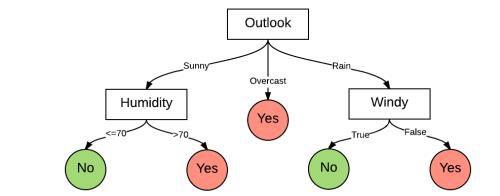
决策树

分类和回归是机器学习领域要解决的最主要的两类问题，前文介绍了很多解决回归问题的方法。除了这些方法外，决策树也是一种可以解决分类问题和回归问题的经典方法，本文重点介绍以决策树解决分类问题。

决策树（decision tree）是一个树结构，可以是二叉树或非二叉树。每个非叶节点表示一个特征属性上的测试，每个分支代表这个特征属性在某个值域上的输出，而每个叶节点存放一个类别。

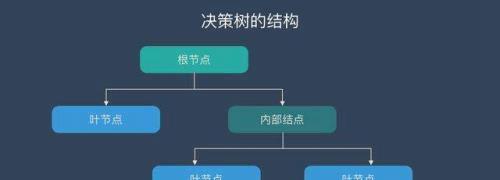
使用决策树进行决策的过程就是从根节点开始，测试待分类项中相应的特征属性，并按照其值选择输出分支，直到到达叶子节点，将叶子节点存放的类别作为决策结果。

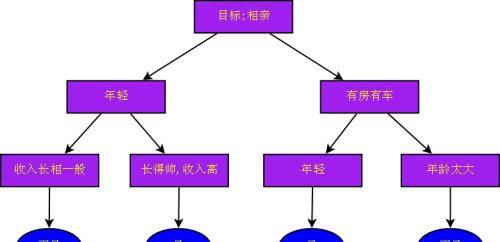
决策树的决策过程

决策树最重要的是决策树的构造。所谓决策树的构造就是进行属性选择度量确定各个特征属性之间的拓扑结构。构造决策树的关键步骤是分裂属性。所谓分裂属性就是在某个节点处按照某一特征属性的不同划分构造不同的分支，其目标是让各个分裂子集尽可能地“纯”。尽可能“纯”就是尽量让一个分裂子集中待分类项属于同一类别。

ID3

教科书上提到最多的决策树算法是ID3算法。信息论中有熵（entropy）的概念，表示状态的混乱程度，熵越大越混乱。

数据样本集S中，样本的分类取值有m种可能（C1，C2，..., Cm），那么总的信息熵就是：

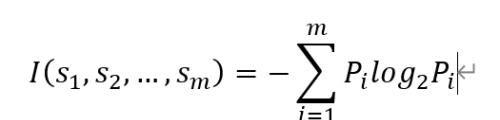
信息熵

其中Pi表示样本属于某一个类别Ci(i在1~m中取值)的概率，si是样本在每一个分类中的数量。

熵的变化可以看做是信息增益，决策树ID3算法的核心思想是以信息增益度量属性选择，选择分裂后信息增益最大的属性进行分裂。

C4.5

但是ID3存在比较大的缺陷，就是选择的时候容易选择一些比较容易分纯净的属性，尤其在具有像ID值这样的属性，因为每个ID都对应一个类别，所以分的很纯净，ID3比较倾向找到这样的属性做分裂。

如果将表格中的第一列ID也作为特征的话，它的信息增益将达到最大值，而这样做显然不对，会造成过拟合。为了减少这种偏好可能带来的不利影响，C4.5算法中将采用信息增益率来进行特征的选择。信息增益率准则对可取值数目较少的属性有所偏好。

数据集D信息增益率的公式为

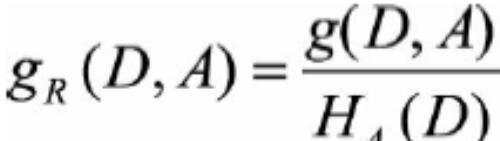
数据集D的信息增益率

其中分母就是分裂熵，H(D)的公式为：

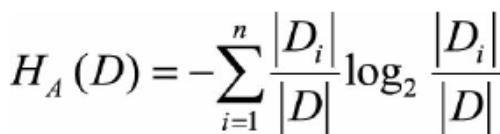
分裂熵

当A的取值越多时，分裂熵越大，信息增益率越小，达到了惩罚的目的。

C4.5相比ID3来说，选择特征并不是看绝对的信息增益有多少，还要看信息增益的过程中，分类取值增加了多少，也就是分裂熵是不是很大。如果是通过增大了很多分裂熵，才换来了一些信息增益，那么其实并不是一种很好的分类方法。

除了C4.5和ID3，目前应用比较多的决策树方法是CART（Classification and Regression Tree），被认为是最佳的决策树模型，sklearn中的决策树也是应用的CART树。

剪枝

当训练数据量大、特征数量较多时构建的决策树可能很庞大，这样的决策树用来分类是否好？答案是否定的。决策树是依据训练集进行构建的，当决策树过于庞大时，可能对训练集依赖过多，也就是对训练集数据过度拟合。从训练数据集上看，拟合效果很好，但对于测试数据集或者新的实例来说，并不一定能够准确预测出其结果。因此，对于决策树的构建还需要最后一步：即决策树的修剪。  决策树的修剪，也就是剪枝操作，主要分为两种：  （1）预剪枝（Pre-Pruning）  （2）后剪枝（Post-Pruning）

预剪枝是指在决策树生成过程中，对每个节点在划分前先进行估计，若当前节点的划分不能带来决策树泛化性能的提升，则停止划分并将当前节点标记为叶节点。

后剪枝是指先从训练集生成一棵完整的决策树，然后自底向上地对非叶节点进行考察，若将该节点对应的子树替换为叶节点能带来决策能力的提升，则将该子树替换成叶节点。

后剪枝决策树通常比预剪枝决策树保留了更多的分支，一般情况下，后剪枝决策树欠拟合的风险很小，其泛化能力往往优于预剪枝预测数。但由于其是基于创建完决策树之后，再对决策树进行自底向上地剪枝判断，因此训练时间开销会比预剪枝或者不剪枝决策树要大。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小迪创作整理编辑！