抽丝剥茧的推理(什么是抽丝剥茧法)

导语：抽丝剥茧，详细解析初中数学题262

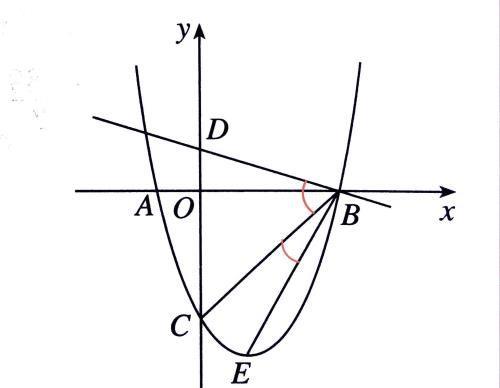
262：如图所示，抛物线y=ax²+bx-3，顶点为E，该抛物线与x轴交于A，B两点，与y轴交于点C，且OB=OC=3OA。直线y=-x/3 +1与y轴交于点D，求∠DBC-∠CBE的度数。

解析：

1.因为△BOC是Rt△，且OB=OC，

所以∠CBO=45°，

如果能够证明∠CBE=∠DBO，

则∠DBC-∠CBE=∠DBC-∠DBO

=45°。

2.因为直线y=-x/3 +1与x轴和y轴分别相交于点B、D两点，

所以有B(3，0)，D(0，1)，

又令x=0，则抛物线y=ax²+bx-3与y轴交点C的坐标为(0，-3)，

所以有OB=OC=3。

又因为OB=OC=3OA，

所以OA=1，

所以A(-1，0)，

所以y=ax²+bx-3

=a(x+1)(x-3)，①

将c(0，-3)代入①式得a=1，

即y=x²-2x-3

=(x-1)²-4，

所以顶点E(1，-4)。

3因为BC=3√2，

CE=√2，BE=2√5，

因为BC²+CE²=BE²，

所以△BCE是直角三角形，

∠BCE=90°，

所以tan∠CBE=CE/CB=1/3。

又在Rt△BOD中，

tan∠DBO=OD/OB=1/3，

所以∠DBO=∠CBE，

所以∠DBC-∠CBE=∠DBC-∠DBO

=45°。

本文内容由快快网络小曲整理编辑！