雷达能够探测多远的距离原来如此简单明了英语(雷达能探测多大的目标)
导语:雷达能够探测多远的距离?原来如此简单明了
知己知彼,百战不殆。
我们对于装备的了解,不能只停留在表面上,光靠眼睛,我们获取的信息是有限的,知其然,更要知其所以然,失之毫厘,谬以千里!一个数据的错误,结果可能千差万别,更何况我们对于装备的了解只停留在表面上,更别谈什么数据了。
关于机载雷达究竟能够探测多远的距离,这一直是我们乐衷于讨论的话题,毕竟一寸长,一寸强,今天我试着从公式的角度来理解雷达探测距离。
假设我们有一个天线,且是全向天线,向着四面八方的空间辐射电磁波(不考虑衰减),天线发射功率为P,天线辐射的距离为R,那么我们需要求出天线发射功率R距离天线距离R处的球面上的功率密度(就是天线辐射在这个球面的平均功率)
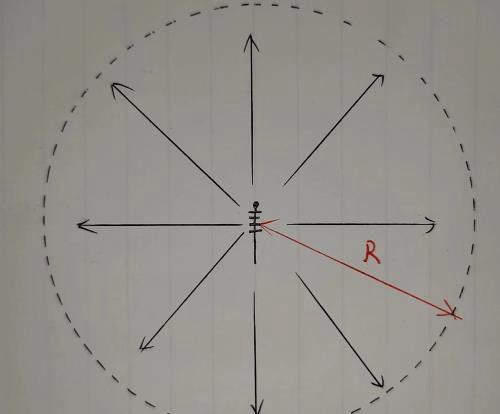
实际上一个全向天线在空间辐射的理想形状是一个球面
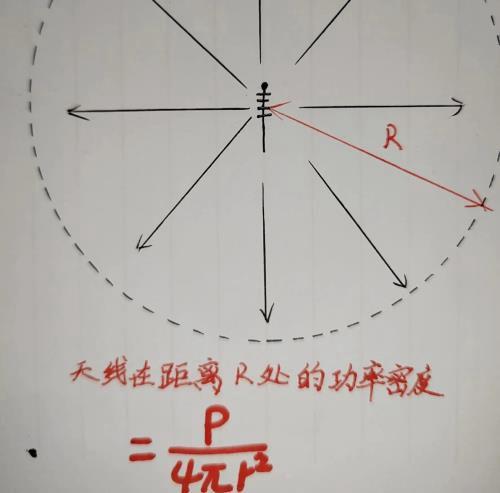
我们要首先要求的就是天线在这个球面上辐射的平均功率,球的面积是4πr^2,这有点类似于求密度一样,用质量÷体积,我们可以将天线辐射功率P看做是质量,球的面积4πr^2看做是体积,那么我们需要求的就是天线在距离R处球面的辐射功率密度。就是P/4πr^2。
为了方便,我们将天线在距离R处的功率密度=S
这是在全向天线的情况下,那我们的机载雷达属于定向天线。如果我们将之前的天线辐射的空间缩小为之前的一半,就如同一个物体,体积为1,质量为1,但我把这个物体的体积压缩到之前的一半,那么这个物体的密度就为2。

同样道理,那么之前天线在距离R处的功率密度就是之前的两倍。
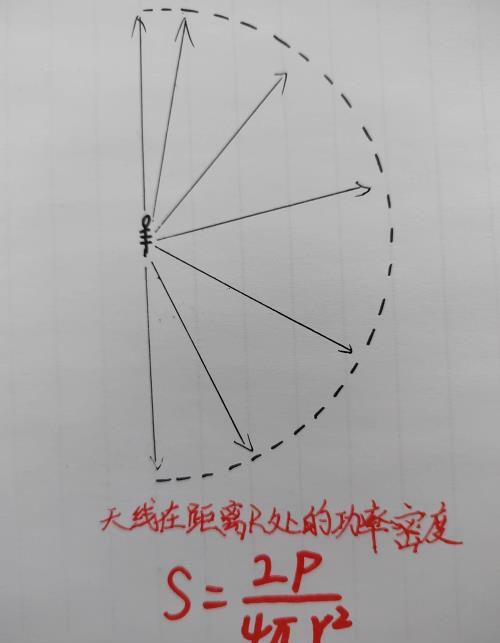
如图所示,功率不变,空间缩小一半,功率密度为之前两倍,相当于在上图空间功率放大了两倍,这就是--增益G
这一种变化我们称之为天线的增益-G(放大倍数),上图的放大倍数就是2,正常来说其他条件相等情况下,天线增益越大,辐射距离越远!

2就是放大倍数,也就是增益G
假设,在距离R处有一个目标,它的雷达反射截面积(RCS)我们设为C,我们将天线距离R处的功率密度(S)×雷达反射截面积C,得到如下公式

左边乘以CRS,右边也要乘以CRS,保持等式相等
这个S•C就是雷达辐射到这个目标上的功率,也就是目标的截获功率。如果不好理解,可以这样想象,你把一盆水落到地上,形成一摊水,这一滩水就是在地面上的的单位面积分布就是S,现在一滩水中有一张纸片,纸片就是目标,水在纸片上的分布就是雷达反射截面积(RCS),你现在就要把单位面积的水S×纸片面积,其实就是这个水截获这张纸片的功率。就是现在这个公式。比喻可能不恰当,希望大家理解。

现在,我们知道了目标截获的功率(上图)
但辐射到目标上的波束还会反射回来,这样我们又回到了第一步的公式,除以一个球的表面积,反射回来的波束还是一球面的形式往回传播。得到如下

这一步其实很好理解,看似麻烦其实和第一步是一样的
其中就是下面这个公式,两边同时除以4πr^2
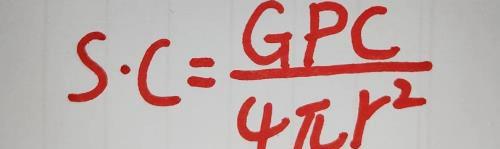
之后反射回来的回波,再被我们的雷达就收到,我们就要用到天线的有效截面积A,将回波的的辐射功率×天线有效截面积A,我们就得到这个公式

我们把接收机所能接收到的最小信号简写成Smin
公式最后变成了这样

两边同时×A
在简写一下
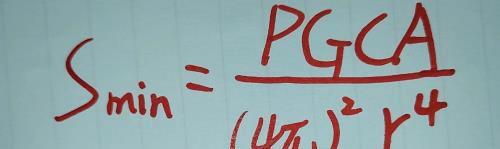
这不是我们最后需要的公式,我们需要把r给提出来,因为这个r才是我们需要的距离,再来变一下得到如下
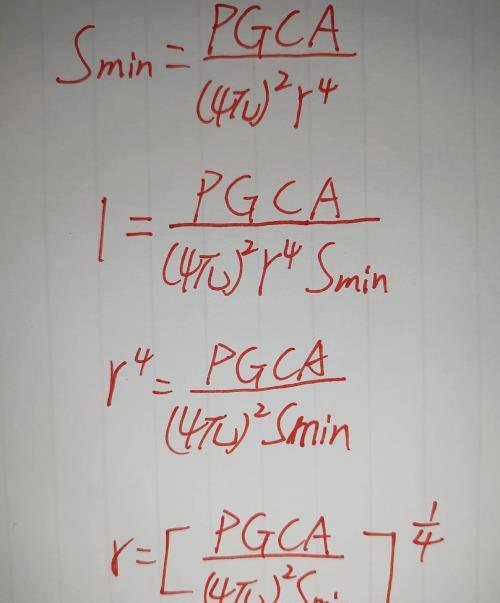
这就是我们需要求的雷达最远探测距离 P是发射功率,G是天线增益,C是目标反射截面积(我们上面说的RCS),A是天线有效截面积Smin是接收的最小信号的功率,r就是圆的的半径,也就是我们需要的雷达最远探测距离!
我们最后来总结一下
第一步

第二步,有了天线放大倍数,就是增益

第三步,辐射到目标上的功率

第四步,辐射到目标上后,在反射回来,又是一个球面,咱又回到了第一步

第五步,咱乘以上天线的有效截面积,这个和第三步又是一样的,相当于目标辐射回来照到我的天线上

第六步,变个式,把r提出来
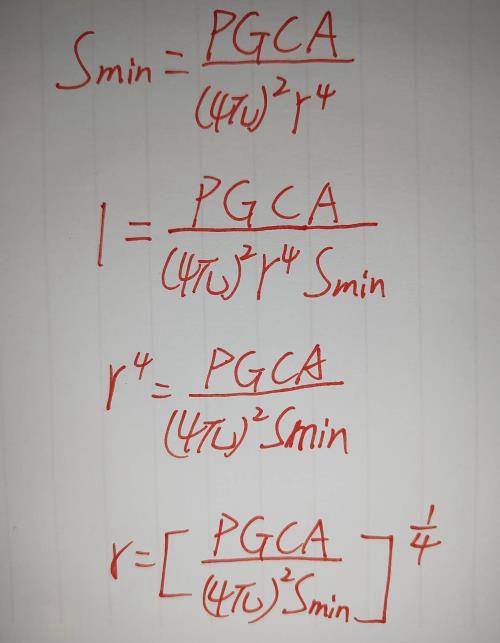
最终的公式
知道这个公式,再想办法搞到其他各项参数,就OK了,其实对于雷达来说,最重要的不是他能探测多远,而是这个雷达的工作频段。
有谁知道任何一部现役雷达的精准工作频段吗,没有人知道,如果你知道,除了造的人,可能就是间谍了!
免责声明:本站部份内容由优秀作者和原创用户编辑投稿,本站仅提供存储服务,不拥有所有权,不承担法律责任。若涉嫌侵权/违法的,请反馈,一经查实立刻删除内容。本文内容由快快网络小茜创作整理编辑!