小数乘整数的算法是什么(小数乘整数计算方法总结)

导语：小数乘整数，计算方法不是重点，更重要的是这个

小数乘整数，是人教版数学五年级上册第一单元第1课时的内容。看课题该属于计算类的，但是，在学习单纯的计算题之前，总是由与之相关的解决问题情境引入，然后列出算式，再通过分析题目中各个数量之间的关系，理清算理。弄清为何这样计算的来龙去脉了，才抛去情境，教学单纯的计算题。因此，本节课的重点是掌握小数乘整数的算理。

因此，本课时的例题1是一道“买风筝”的解决问题：主题图的信息是一位阿姨在卖风筝，风筝的价格有4.6元、3.5元、6.4元、2.8元这四种，三个孩子要买3个3.5元的风筝，需要多少钱？

首先，得让孩子说出此题的数量关系：单价×数量=总价，知道单价和数量，计算总价用乘法计算：3.5×3=

然后，让学生估一估：买3个3.5元的风筝，大概要带多少钱。估算能力在日常生活中经常能用到（比如买衣服，买文具等，父母给多少钱合适），所以平时教学中应经常渗透估算的意识。此题中，把“3.5元”估计成“4元”，结果是4×3=12（元），带12元合适。为什么不能估计成3元呢？因为买东西，钱可以多带点，但不能少带，少了就不够买了，这个道理孩子们前面接触过。

第三步，让孩子们用自己的方法来解决这道题，可能会出现下面三种解题思路。

第一种：用分解组合法计算。把3.5元换算成3元5角；然后分别算3个3元是9元，3个5角等于1元5角；再把两部分加起来9元+1元5角=10元5角。

第二种：用加法竖式计算。因为在四年级下册，孩子们学习了小数的加减法，3个3.5相加，也可以列成加法算式，用竖式计算得出：3.5+3.5+3.5=1.5（元）。

第三种：把小数乘法转化为整数乘法计算。这种“转化”用的是将“新知”转化为“旧知”的思路进行教学的，也是帮助孩子理解小数乘整数算理的关键步骤。将3.5元换算成35角，这样，以“元”为单位时，数据3.5是一个一位小数；而以“角”为单位时，这只风筝应该是35角，35是整数。这样就把小数乘整数的算式3.5×3，转化,为整数乘整数的算式35×3了。整数乘整数的竖式计算以前学过，口算都没有问题，算出35×3=105角之后，再把得数105角换算成10.5元。

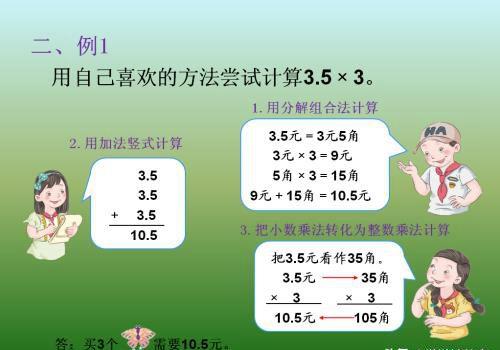
把 “3.5×3”和“35×3”的两个竖式都列出来，用箭头的方法表示出转化的步骤，这样，可以比较得出：小数乘整数中，有一个因数是几位小数，积也是几位小数。

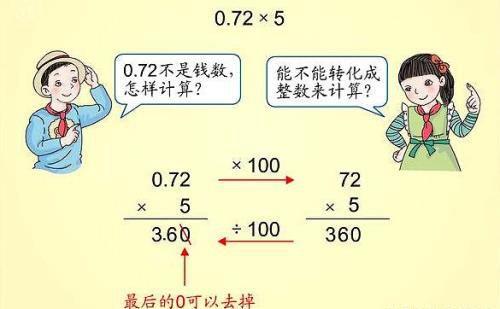
例1是通过人民币的单位“元”和“角”的换算，帮助学生理解小数乘整数的竖式计算的算理的。而“例2”就完全脱离了解决问题的情境，单纯计算0.72×5这道题了。

此题也可以通过把小数乘法的算式转化成整数乘法的算式来列竖式计算。没有了单位换算，可以用移动小数点的位置来入手，即0.72变成整数72，小数点要向右移动两位，也就是×100，然后用竖式计算72×5=360，返回0.72×5的话，积360得把小数点向左移动两位，也就是÷100，得3.60。这里，根据小数的基本性质，3.60末尾的“0”可以去掉。

因此，小数乘法中，积的小数部分末尾如有0，可以根据小数的基本性质去掉小数末尾的0，而整数乘法中末尾的0是不能去掉的。

综合上述，小数乘整数与整数乘整数的不同点有两点：①小数乘整数中，有一个因数是几位小数，积也是几位小数。②小数乘法中，积的小数部分末尾如有0，可以根据小数的基本性质去掉小数末尾的0，而整数乘法中末尾的0是不能去掉的。

由此，可以归纳出小数乘整数的计算方法：①把小数乘整数转化为整数乘法，按整数乘法的规则进行计算；②处理好小数点的位置。看因数中共有几位小数，就从积的右边起数出几位，点上小数点。（积的小数部分末尾的0可以去掉。）

明白了“小数乘整数”的算理和计算方法了，后面“小数乘小数”的问题就迎刃而解了。所以，第2课时“小数乘小数”的内容也同样可以用“转化”的思想去解决。在这里把题目给你：给一个长2.4米、宽0.8米的长方形宣传栏刷油漆，每平方米要用油漆0.9千克。一共需要多少千克油漆？

开学要上五年级的小朋友，你会做么？快来试一试吧

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小奈创作整理编辑！