1/cosx的原函数是多少

1／cosx的原函数是ln｜secx＋tanx｜＋c。解答如下：

先算1／sinx原函数，s表示积分号

s1／sinxdx

＝s1／（2sin（x／2）cos（x／2））dx

＝s1／［tan（x／2）cos²（x／2）］d（x／2）

＝s1／［tan（x／2）］d（tan（x／2））

＝ln｜zhitan（x／2）｜＋c

因为tan（x／2）＝sin（x／2）／cos（x／2）＝2sin²（x／2）／［2sin（x／2）cos（x／2）］＝（1－cosx0／sinx＝cscx－cotx

所以s1／sinxdx＝ln｜cscx－cotx｜＋c

s1／cosxdx

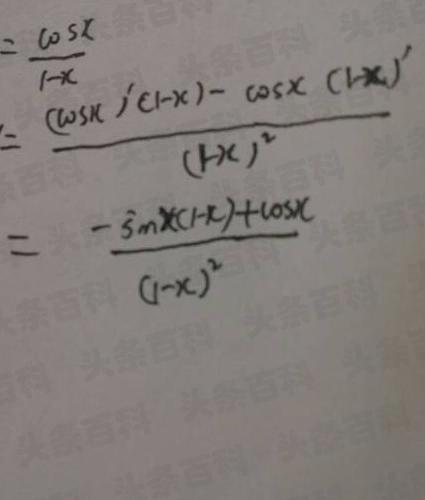
＝s1／sin（x＋派／2）d（x＋派／2）

＝ln｜csc（x＋派／2）－cot（x＋派／2）｜＋c

＝ln｜secx＋tanx｜＋c