导语：升幂、降幂、二倍、半角这些绕晕你的变换你会吗？

考纲原文

1．和与差的三角函数公式

（1）会用向量的数量积推导出两角差的余弦公式.

（2）能利用两角差的余弦公式导出两角差的正弦、正切公式.

（3）能利用两角差的余弦公式导出两角和的正弦、余弦、正切公式，导出二倍角的正弦、余弦、正切公式，了解它们的内在联系.

2．简单的三角恒等变换

能运用上述公式进行简单的恒等变换（包括导出积化和差、和差化积、半角公式，但对这三组公式不要求记忆）.

知识点详解

一、两角和与差的三角函数公式

1．两角和与差的正弦、余弦、正切公式

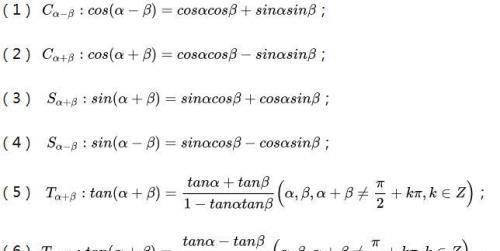
2．二倍角公式

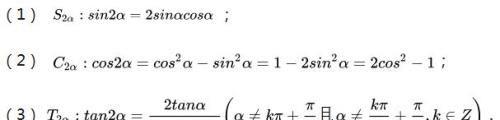
3．公式的常用变形

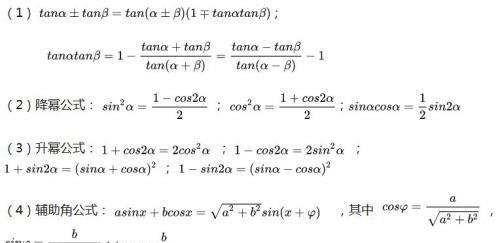
二、简单的三角恒等变换

1．半角公式

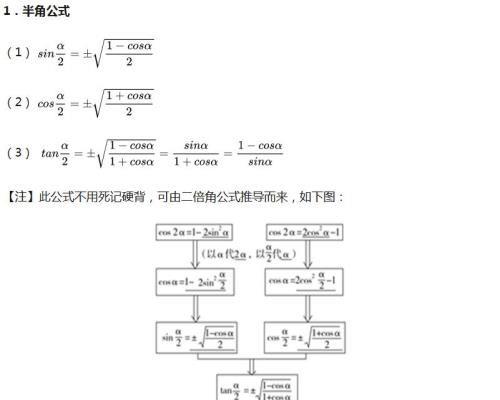
2．公式的常见变形（和差化积、积化和差公式）

考向分析

考向一 三角函数式的化简

1．化简原则

（1）一看角之间的差别与联系，把角进行合理的拆分，正确使用公式；

（2）二看函数名称之间的差异，确定使用的公式，常见的有“切化弦”；

（3）三看结构特征，找到变形的方向，常见的有“遇到分式要通分”，“遇到根式一般要升幂”等．

2．化简要求

（1）使三角函数式的项数最少、次数最低、角与函数名称的种类最少；

（2）式子中的分母尽量不含根号.

3．化简方法

（1）切化弦；

（2）异名化同名；

（3）异角化同角；

（4）降幂或升幂．

【方法技巧】

(1)三角化简的常用方法：异名三角函数化为同名三角函数，异角化为同角，异次化为同次，切化弦，特殊值与特殊角的三角函数互化．

(2)三角化简的标准：三角函数名称尽量少，次数尽量低，最好不含分母，能求值的尽量求值．

(3)在化简时要注意角的取值范围.

考向二 三角函数的求值问题

1．给角求值

给角求值中一般所给出的角都是非特殊角，从表面上来看是很难的，但仔细观察会发现非特殊角与特殊角之间总有一定的关系．解题时，要利用观察得到的关系，结合公式将非特殊角的三角函数转化为特殊角的三角函数，从而得解.

2．给值求值

已知三角函数值，求其他三角函数式的值的一般思路：

（1）先化简所求式子．

（2）观察已知条件与所求式子之间的联系(从三角函数名及角入手)．

（3）将已知条件代入所求式子，化简求值．

3．给值求角

通过求角的某种三角函数值来求角，在选取函数时，有以下原则：

（1）已知正切函数值，则选正切函数．

4．常见的角的变换

（1）已知角表示未知角

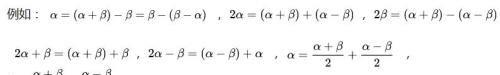
（2）互余与互补关系

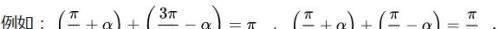
（3）非特殊角转化为特殊角

例如：15°=45°−30°，75°=45°＋30°.

【名师点睛】

解给值求值型问题的一般思路是：先看公式中的量,哪些是已知的,哪些是待求的,再利用已知条件结合同角三角函数的基本关系求出待求值,注意根据角的象限确定符号. 这类求值问题关键在于结合条件和结论中的角，合理拆、配角.

考向三 三角恒等变换的综合应用

1．与三角函数的图象及性质相结合的综合问题

（1）利用三角恒等变换及辅助角公式把三角函数关系式转化成y=Asin(ωx＋φ)＋t或y=Acos(ωx＋φ)＋t的形式．

（3）根据自变量的范围确定ωx＋φ的范围，根据相应的正弦曲线或余弦曲线求值域或最值，另外求最值时，根据所给关系式的特点，也可换元转化为二次函数的最值．

（4）根据正、余弦函数的单调区间列不等式求函数y=Asin(ωx＋φ)＋t或y=Acos(ωx＋φ)＋t的单调区间．

2．与向量相结合的综合问题

3．与解三角形相结合的综合问题

（1）利用正弦定理把边的关系化成角，因为三个角之和等于π，可以根据此关系把未知量减少，再用三角恒等变换化简求解；

（2）利用正、余弦定理把边的关系化成角的关系再用三角恒等变换化简求解．

【注】此类题中的角是在三角形中，每个角范围限制在(0，π)内，如果是锐角三角形，则需要限制各个角均在 内．角的范围在解题中至关重要，做题时要特别注意.

【名师点睛】

三角函数求值的三种类型

（1）给角求值：关键是正确选用公式，以便把非特殊角的三角函数转化为特殊角的三角函数．

（2）给值求值：关键是找出已知式与待求式之间的联系及函数的差异．一般有如下两种思路：①适当变换已知式，进而求得待求式的值；②变换待求式，便于将已知式的值代入，从而达到解题的目的．

（3）给值求角：实质是转化为“给值求值”，先求角的某一函数值，再求角的范围，进而确定角．

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小畅创作整理编辑！