七上线段中点问题题型讲解(七年级数学线段中点专题)

导语：七年级上学期，数学期末复习之线段中点问题专题训练，三种题型

七年级上学期，数学期末复习之线段中点问题专题训练，三种题型。我们先看一下线段中点的基本概念，如图，点M把线段AB分成相等的两条线段AM与BM，点M叫做线段AB的中点。

几何语言：∵M是线段AB的中点

∴AM= MB=1/2AB (或AB=2AM=2MB)

反之也成立：∵AM=MB =1/2AB (或AB=2AM=2MB)

∴M是线段AB的中点.

类似的，还有线段的三等分点，四等分点。线段的中只有1个，且一定在线段上。若点C是线段AB的中点，则AC= BC；但若AC=BC，点C不一定是线段AB的中点。

01单个中点问题

例题1：如图，已知DB=2，AC=10，点D为线段AC的中点，求线段BC的长度．

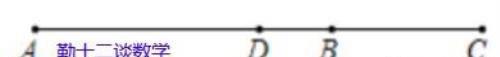
分析：根据线段中点的性质推出DC=AD=1/2AC=1/2×10=5，再结合图形根据线段之间的和差关系进行求解即可。

本题考查两点间的距离，解题的关键是根据线段中点的性质推出DC=AD=1/2AC，注意数形结合思想方法的运用。

例题2：如图，延长线段AB到C，使BC=3AB，点D是线段BC的中点，如果CD=9cm，那么线段AC的长度是多少？

分析：已知CD的长度，CD是线段BC的一半，则BC长度可求出，根据3AB=BC，即可求出AB的长度，进而可求出AC的长度．

解：∵点D是线段BC的中点，CD=9cm，∴BC=18cm，∵BC=3AB，∴AB=6cm，AC=AB+BC=18+6=24cm．

例题3：已知点C在直线AB上，M是AC的中点，点N在线段CB上，且NC：NB=1：2．

（1）如图，点C在线段AB上，若AC=14，BC=12，求线段MN的长；

（2）若AC=a，BC=b，求线段MN的长．

分析：（1）根据线段中点的定义和线段的和差即可得到结论；（2）①若点C在线段AB上，②若点C在AB的延长线上，③若点C在BA的延长线上，根据线段中点的定义和线段的和差即可得到结论．

本题考查了两点间的距离，利用了线段中点的性质，线段的和差。

02无关联型双动点问题

例题4：如图，点M是AB的中点，点N是BD的中点，AB=8cm，BC=12cm，CD=6cm．（1）求BM的长；（2）求AN的长．

分析：（1）根据线段中点的性质直接可得出BM的长；（2）根据线段中点的性质推出BN=DN=1/2BD，进而结合图形根据线段之间的和差关系进行求解即可．

本题考查两点间的距离，解题的关键是根据线段中点的性质推出BM=AM=1/2AB，BN=DN=1/2BD，注意数形结合的运用。

例题5：如图，已知线段AB上有两点C，D且AC：CD：DB=2：3：4，点E、F分别为AC，DB的中点，EF=18厘米．求AB的长．

分析：设AC=2a cm，得出CD=3a cm，DB=4a cm，然后根据E、F分别是线段AC、DB的中点，分别用a表示出EC、DF，根据EF=18，求出a的值，即可求出线段AB的长。

此题主要考查了两点间的距离的求法，以及线段的中点的特征和应用，要熟练掌握。

例题6：如图，C为线段AB上一点．AB=m，BC=n，M，N分别为AC，BC的中点．（1）若m=8，n=2，求MN的长；（2）若m=3n，求CN/MN的值．

分析：根据M，N分别为AC，BC的中点可得MC=12AC，NC=12BC，进而可求MN的值，第2小问用含n的式子表示CN和MN即可求解．

本题考查了两点间的距离，解决本题的关键是利用线段中点定义。

03关联型双中点问题​

例题7：如图，点C为线段AB的中点，点E为线段AB上的点，点D为线段AE的中点，若AB=15，CE=4.5，求出线段AD的长度．

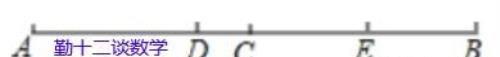
分析：根据中点的性质，可得BC的长，根据线段的和差，可得BE的长，AE的长，根据中点的性质，可得答案．

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小芦创作整理编辑！