k均值算法原理(k均值算法思想及优缺点)

导语：机器学习系列20：K-均值算法

机器学习系列20：K-均值算法

曾经我写过一篇文章介绍监督学习和无监督学习的区别与特点，如果没看过的小伙伴可以看一下：

机器学习系列 1：监督学习和无监督学习

接下来介绍的K-均值算法就是无监督学习算法。在无监督学习中，我们会把没有标签的数据集交给算法，让它自动地发现数据之间的关系，聚类算法(Clustering algorithm)就是一种无监督学习算法。它会自动地将无标签的数据集进行分类，如下图：

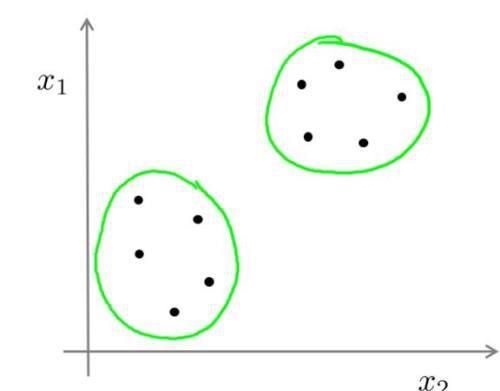
它会将这个数据集划分成两类，每一个绿圈就是一类。

在聚类算法中，最常见的就是 K-均值算法(K-means algorithm)，我们先来看看这个算法在下面这个数据集中是如何进行工作的。

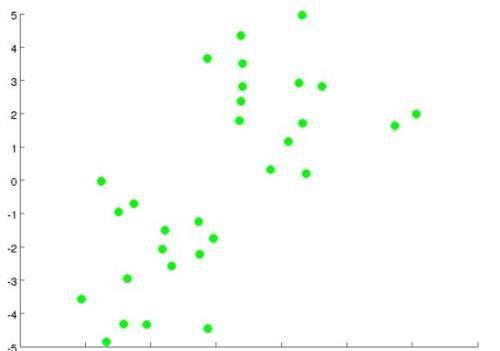
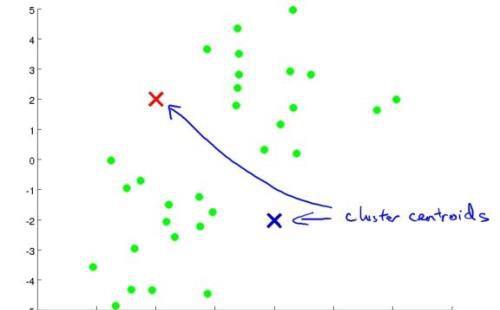
如果将数据集划分成两类的话，第一步随机选取两个点作为聚类中心(通常不是这么选择，为了更方便的理解，先这么选，在后面我会告诉你正确应该如何去选择)：

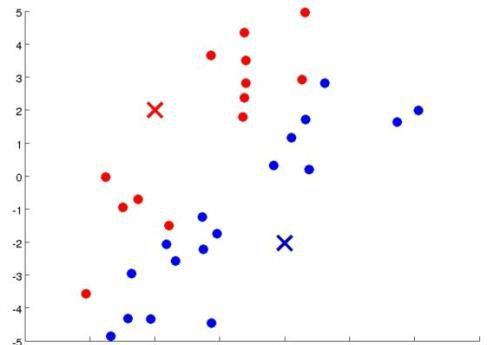
对于每一个样本点，离哪一个聚类中心近就会被染成相应的颜色，划归成相同的一类：

然后每一类都会计算出离那些数据集最近的一个位置，将聚类中心移动到那个位置：

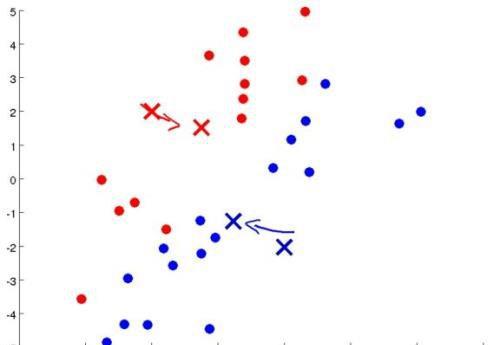
之后再进行染色：

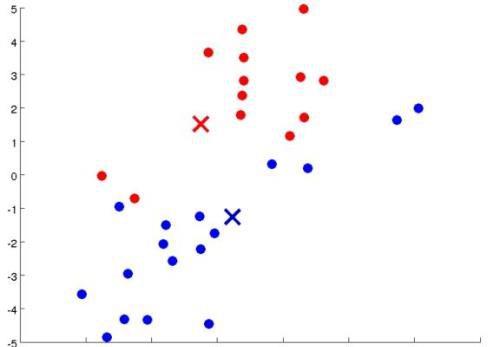
再移动，再染色，再移动，再染色，再移动。。。(人类的本质是什么

)不断地进行循环，直到聚类中心不再移动为止：

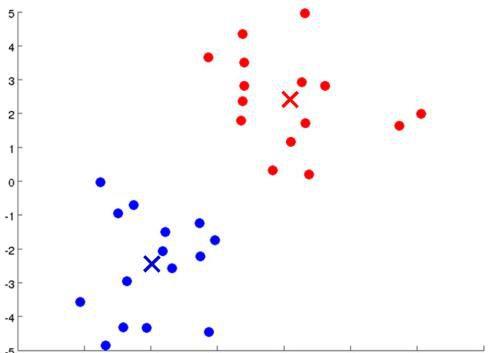
现在就成功地划分出两类不同的数据集了。

再回过头来看 K-均值算法(K-means algorithm)：它需要传入两个参数，需要聚类的数量 K 和训练集。

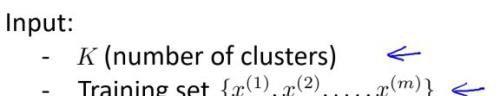
一开始，会根据传入聚类的数量 K 随机初始化聚类中心，然后不断地去循环内部的两个循环：

红色部分表示每一个样本点选择离它最近的聚类中心染成相应的颜色，也就是簇分配，我们将每一个样本点划分到所属的聚类中心。实际上就是最小化这个代价函数：

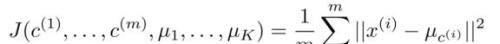
蓝色部分表示不断地去移动聚类中心使它到跟它颜色相同的样本点的距离最小。

最后来补充一下如何初始化聚类中心。之前说过，随机位置初始化这种方法是不可取的，正确的操作是随机选取样本点所在的位置作为聚类中心，为了避免陷入到局部最优解中，我们要多次选取，挑选一个代价函数最小的作为我们的选择，这样就会达到最优的效果。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小萱创作整理编辑！