高中函数单调性怎么求(高中数学函数单调性讲解)

导语：有了此宝典，高中函数单调性的问题不再怕啦！

在上一节中我们讲了函数的周期性的相关知识，接下来我帮大家梳理一下函数的单调性的相关的学习重点、学习方法以及常见的题型及应对办法。首先，我们要对函数的单调性有一个比较深刻的认识。在理解函数的单调性的时候我们要注意三点①函数的单调性是对于函数的某个区间成立的。意思说的是，我们在描述一个函数的单调性的时候，一定要指出这个函数满足单调性的区间。

对于这样的分段函数，我们不能笼统的说是一个增函数或者是一个减函数，只能在不同区间范围内去证明的单调性特点。其实这里体现的就是一个教育的理念，就像我们在生活中要能够判断是非曲直一样，在数学里，我们也要具备区分选择标准的能力。②函数的单调性强调的是一个任意性，即在给定的区间内，都满足条件。③函数的单调性不仅是函数图像的表现，也是代数关系的体现。其次，就是对函数的单调性的判断。函数的单调性的判断常见的方法就是定义法、图象法、公式法和求导法。这些方法说起来很单调，但是都是很实用的方法。其中，定义法常用来解决一些基础的显函数（即有函数表达式的单调性的证明）的单调性问题。而图象法则常常要求我们能够根据函数的图像，能够结合代数式，进行判断。公式法和求导法则常用来进行函数的参数的范围的求解、不等式的证明以及在构造函数中用到。在高三阶段，我们尤其要对求导法和公式法进行深刻的理解，在做题中加以体会、消化。最后，讲一下函数的单调性究竟可以用来干什么。我们知道，函数是将我们的代数知识和几何知识连接起来的桥梁。因此，从这个角度出发，我们画函数图像的时候，如果能够对这个函数的特点有更多的了解的话，肯定能更加准确的画出这个函数的图像。所以，函数的第一个用途就是准确的画出函数的图像。如果在遇到问题的时候，我们能准确的画出函数的图像，可以更多的帮助我们去思考问题，去做出判断。比如下面这个填空题已知函数是定义域为R的偶函数，

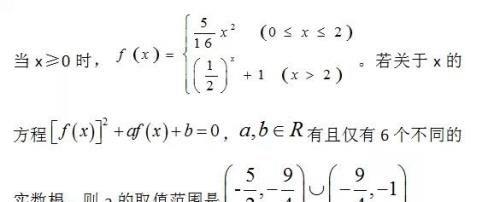
这道题是一道典型的利用函数的单调性理解函数的特征，然后从函数的图像中寻找突破口的问题。其解题的方法如下：首先，我们根据题意将二次函数、指数函数的在Y轴右侧的图像画出来，然后再根据偶函数的特点将函数的左边的图像画出来。如下图所示。

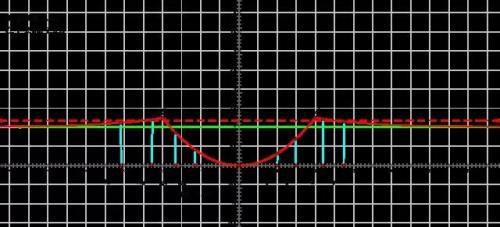
有6个不同的函数解，那么只需要保证在Y轴的右侧有三个不同的解就可以了。首先，我们知道，得到的方程的解是函数的值，然后再通过函数的值来对应相应的的x的值。从而，通过观察函数的图像，

从上述这个例子，可以看出，如果我们能够根据函数的单调性将函数的图像画出来，对于解决问题的帮助有多大了。在学习函数的单调性的时候，我们不能忘了一个基本的概念，那就是函数的单调性是一个符号性的东西，是可以进行必要的代换的。这也是符合函数告诉我们的东西。在接下来的专题中，我会通过例题的形式向大家来讲述。概况近几年高考中出现的有关函数的问题，经常会用到函数的单调性进行必要的判断。我们要养成用单调性分析函数的意识，不断提高自己的能力！

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小思创作整理编辑！