如何证明三角形三条中线交于一点

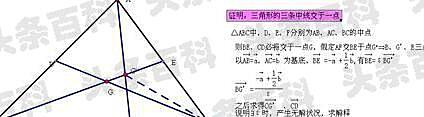
在△abc中，bd为ac中线，ce为ab中线，bd、ce交于点o，证bc的中线af过点o；

延长ao交bc于f'，作bg平行ec交ao延长线于g，则因e为ab中点，所以o为ag中点；

连接gc，则在三角形agc中，od是中位线，bd平行gc，所以bocg为平行四边形；

f'平分bc，f'与f重合。bc的中线af过点o。

三角形中线的性质：

1、三角形中中线的交点为重心，重心分中线为2：1（顶点到重心：重心到对边中点）。

2、在一个直角三角形中，直角所对应的边上的中线为斜边的一半。

3、任意三角形的三条中线把三角形分成面积相等的六个部分。中线都把三角形分成面积相等的两个部分。除此之外，任何其他通过中点的直线都不把三角形分成面积相等的两个部分。