利用特殊四边形的性质巧解折叠问题(特殊四边形折叠问题教学设计)

导语：「初二数学」利用特殊四边形的性质巧解折叠问题

四边形的折叠问题是指将四边形按照某种方式折叠，然后在平面图形内按照要求完成相应的计算和证明，折叠的本质是图形的轴对称变换，所用关系是折叠后的图形与原图形全等，解题方法大多是列方程的方法.

一.平行四边形的折叠问题

1.如图，将平行四边形ABCD沿对角线AC折叠，使点B落在点B'处，若∠1=∠2=44°，求∠B的度数.

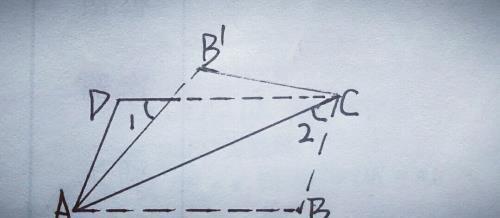
【分析】由折叠知，∠CAB=∠CAB'=1/2∠BAB'，又∵平行四边形ABCD，AB∥CD，∴∠1=∠BAB'，∵∠1=∠2=44°，∴∠CAB=22°，在△ABC中，可得∠B=180°一44°一22°=114°.

2.如图，将平行四边形纸片沿对角线AC所在直线折叠，点D落在点E处，AE恰好经过BC边的中点F，若AB=3，BC=6，求∠B的度数.

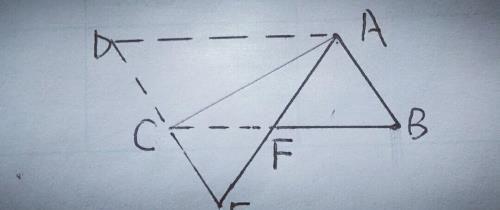
【分析】由折叠知，∠DAC=∠EAC，而四边形ABCD是平行四边形，AD∥BC，∴∠DAC=∠ACB，∴∠EAC=∠ACB，∴AF=CF，而F为BC的中点，CF=BF=3，∴AF=BF=3，又∵AB=3，∴△ABF为等边三角形，∴∠B=60°.

二，矩形的折叠问题

3.如图，在矩形ABCD中，AB=10，BC=5，点E，F分别在AB，CD上，将矩形ABCD沿EF折叠，使点A，D分别落在矩形ABCD外部的点A1，D1处，求阴影部分图形的周长.

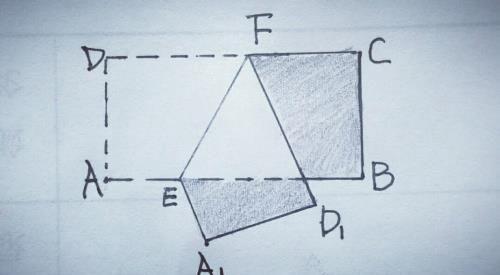
【分析】由折叠性质知，DF=D1F，AE=A1E，AD=A1D1，阴影部分图形的周长=D1F+FC+BC+BE+A1E+A1D1=(DF+FC)+BC+(BE+AE)+AD=DC+BC+AB+AD=矩形ABCD的周长=2×10+2×5=30.

4.如图，把矩形纸片ABCD折叠，使点B落在点D处，点C落在点C'处，折痕EF与BD交于点O，已知AB=16，AD=12，求折痕EF的长.

【分析】由已知条件，得∠C'DF=∠CDA=90°，∴∠C'DE=∠ADF，∵∠A=∠C=∠C'=90°，AD=BC=DC'，∴△DAF≌△DC'E，∴DF=DE=BF，∵四边形ABCD是矩形，∴AB∥CD，连接BE，则四边形DFBE是菱形，如图，

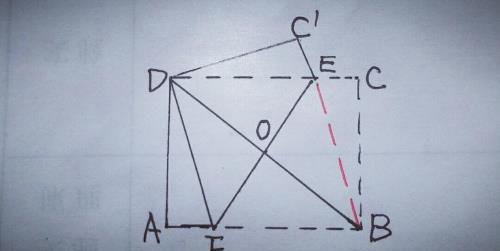
∴OB=OD，OE=OF，BD⊥EF，设AF=x，则DF=BF=16一x，在Rt△DAF中，AD²+AF²=DF²，∴12²+x²=(16一x)²，解得x=7/2，∴DF=25/2，在Rt△ABD中，BD²=AD²+AB²，可得BD=20，∴DO=10，在Rt△DOF中，可算出OF=15/2，∴EF=2OF=15.

三.菱形的折叠问题

5.如图，在菱形ABCD中，∠A=120°，E是AD上的点，沿BE折叠△ABE，点A恰好落在BD上的F点，连接CF，求∠BFC的度数.

【分析】∵四边形ABCD是菱形，∠A=120°，∴∠ABC=60°，∴∠FBC=30°，由折叠性质得，AB=BF，∴BF=BC，在△BFC中，可求得∠BFC=75°.

6.如图，将菱形纸片ABCD折叠，使点A恰好落在菱形的对角线交点O处，折痕为EF，若菱形的边长为2，∠A=120°，求EF的长.

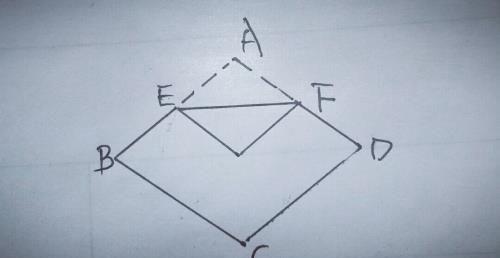
【分析】连接BD，AC，如图，

∵四边形ABCD是菱形，∴AC⊥BD，AC平分∠BAD，∵∠BAD=120°，∴∠BAC=60°，∴∠BAO=30°，∴AO=AB/2=1，在Rt△AOB中，可算出BO=√3，∵点A沿EF折叠与点O重合，∴EF⊥AC，∵BD⊥AC，∴EF∥BD，∴EF为△ABD的中位线，∴EF=BD/2=BO=√3.

四.正方形的折叠问题

7.如图，正方形纸片ABCD的边长AB=12，E是DC上的一点，CE=5，折叠正方形纸片使点B和点E重合，折痕为FG，求FG的长.

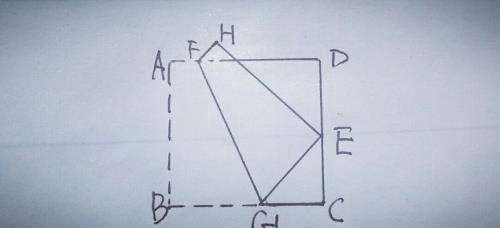
【分析】由折叠性质知FG⊥BE，过点F作FM⊥BC于M，设BE交FG于N，如图，

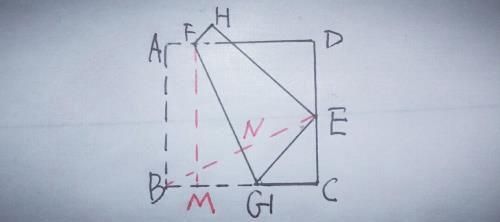
则∠C=∠BNG=90°，∠BGN=∠BEC，又可知FM=BC，∠FMG=∠C，∴△FMG≌△BCE，∴FG=BE，在Rt△BEC中，可求得BE=13，∴FG=13.

8.如图，有一张边长为4的正方形纸片ABCD，点P为正方形AD边上的一点(不与点A，点D重合)，将正方形纸片折叠，使点B落在P处，点C落在G处，PG交DC于H折痕为EF，连接BP，BH.

(1)求证:∠APB=∠BPH;

(2)当点P在边AD上移动时，△PDH的周长是否发生变化？并证明你的结论.

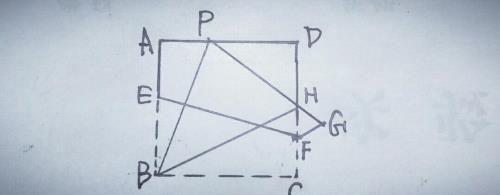
【分析】(1)由折叠知，PE=BE，∠EPB=∠EBP，而∠EBC=∠EPG=90°，∴∠BPH=∠PBC，又∵AD∥BC，∴∠APB=∠PBC，∴∠APB=∠BPH.

(2)△PDH的周长不变，且为定值8.理由如下:

由(1)知∠APB=∠BPH，∴过B作BQ⊥PH于Q，如图，

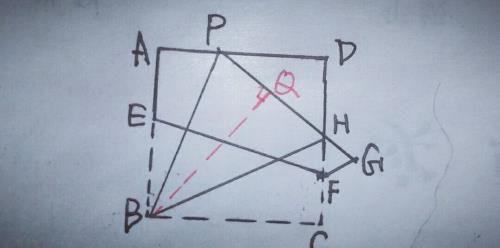
∵∠A=∠BQP=90°，BP=BP，∴△ABP≌△QBP，∴AP=QP，AB=BQ，∵AB=BC，∴BQ=BC，又∵∠C=∠BQH，BH=BH，∴Rt△BCH≌Rt△BQH，∴CH=QH，∴△PDH的周长=PD+DH+PH=PD+DH+AP+HC=AD+DC=8.

【总结】

折叠问题，题型多变，关键是利用轴对称的性质，抓住背景图的性质，运用方程的思想，函数的思想，转换的方法从而解题.折线是对称轴，对应点的连线段被对称抽垂直平分，折叠前后的图形全等.

感谢大家的关注、转发、点赞、交流！

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小姿创作整理编辑！