集合子集个数公式如何证明

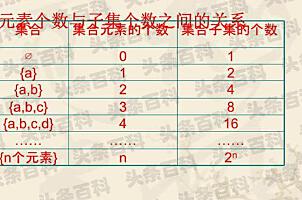
如果一个集合的元素有n个，那么它的子集有2的n次方个（注意空集的存在），非空子集有2的n次方减1个，真子集有2的n次方减1个，非空真子集有2的n次方减2个。

如果元素少的话可以用枚举法，不过最好的方法还是用二项式定理做。

例如：已知一个集合里有n个元素（下面的c代表组合，其中ncr代表从n个元素内选取r个元素进行组合）

首先子集中元素有0个的有[nc0]

子集元素有1个的有[nc1]

子集元素有2个的有[nc2]

……

子集元素有m个的有[ncm]

……

子集元素有n-1个的有[nc（n-1）]

子集元素有n个的有[ncn]

所以一个有限集合内有[nc0]+[nc1]+[nc2]+……+[ncm]+……+[nc（n-1）]+[ncn]