跳动公差含义(跳动公差采用的公差原则)

导语：跳动公差(二)

跳动公差的基准一定是基准轴，而控制的对象可以是绕基准轴旋转而成，或是与基准轴垂直。这两种情况分别有各自的数学定义。

这次讨论绕基准轴旋转而成的情况。这样形成的表面可以平行于基准轴，或是与基准轴成非90度角（设想一下圆锥体）。图1展示了这两种情况。此时的公差带通过让长度等于公差值t0（图1中为0.15）、并且与所控制表面垂直的线段绕轴线旋转而成。容易看出，这样得到的公差带，要么是圆环面（红色），要么是圆锥台的侧表面（绿色）。

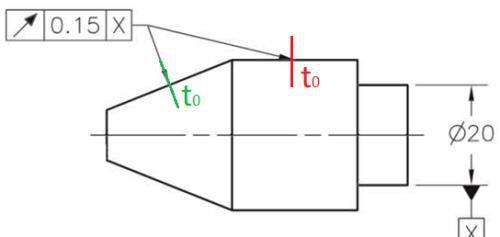
图1. 控制面与轴线平行或成角度（不是直角）

用数学语言来表述，则是满足如下向量式的所有点P带->的集合：

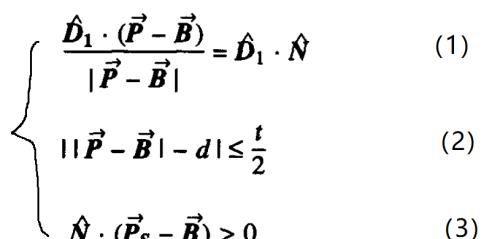
绕轴线旋转而成的圆跳动公差的数学表达式

其中点A带->（这个点在数学式中没有出现，但在确定点B带->时要用到，因为点B带->是一个交点）和方向向量D1带^代表基准轴线。Ps带->（P是英文点Point的首字母，s是英文表面Surface的首字母。这样理解起来方便）是所控制表面上的任一点。N带^（N是英文法线Normal的首字母）是通过点Ps带->的法向向量，其方向根据所控制表面的配合面来确定。B带->是基准轴和下述直线的交点：该直线经过点Ps带->并且平行于方向向量N带^。d(d是英文距离distance的首字母)是点B带^到公差带中心的距离，且表示这个距离的线段要平行于N带^。t（t是英文公差tolerance的首字母）是公差带的大小，且表示这个大小的线段也要平行于N带^。

式(1)的几何意义：与N带^重叠的直线上的所有点。

式(2)的几何意义：从式(1)中的直线取出一段，该线段长度等于t，且在d的两侧对称分布。

式(3)的几何意义：N带^和(Ps带-> - B带->)之间的夹角为0度和锐角，但不能是直角90度。0度代表与基准轴线平行的情况，锐角代表与基准轴线成倾斜夹角的情况。而直角90度将变成与基准轴垂直，属于圆跳动公差的第一种情形，详见。

结合图2，有助于更好地理解各向量式的含义。

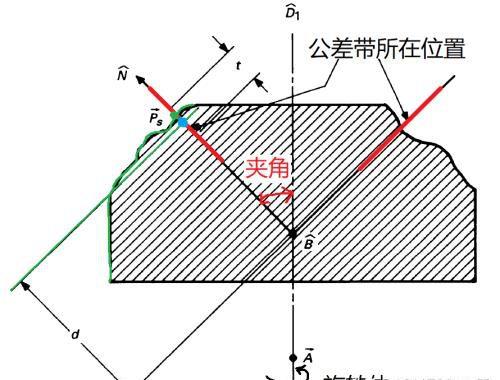
图2. 圆跳动公差图解

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小冰创作整理编辑！