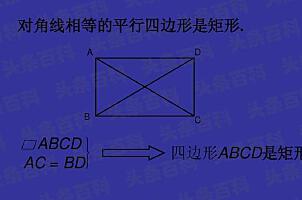
对角线相等的平行四边形是矩形吗

是矩形。矩形的判定方法有：有一个角是直角的平行四边形是矩形；对角线相等的平行四边形是矩形；有三个角是直角的四边形是矩形；对角线相等且互相平分的四边形是矩形。所以，对角线相等的平行四边形可以证明是矩形。

设ac、bd是平行四边形abcd的对角线，ac=bd，求证：四边形abcd是矩形。

证明：

∵四边形abcd是平行四边形，

∴ab=dc（平行四边形对边相等），

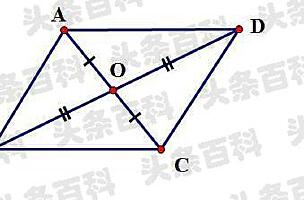
又∵ac=bd，bc=cb，

∴△abc≌△dcb（sss），

∴∠abc=∠dcb，

∵ab//dc（平行四边形对边平行），

∴∠abc+∠dcb=180°（两直线平行，同旁内角互补），

∴2∠abc=180°（等量代换），

∴∠abc=90°，

∴四边形abcd是矩形（矩形定义：有一个角是直角的平行四边形是矩形）。