神奇的印度速算方法介绍(二)(印度速算法害处很大)

导语：从神奇的印度速算法说起

第一章 快速了解速算法

介绍一个两位数乘法心算的方法——神奇的印度速算法，从高位算到低位，迅速准确，适合心算。请看下图：

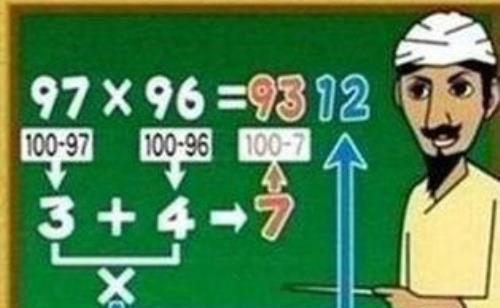
计算步骤如下：

① 97的补数是3；

② 96的补数是4；

③ 两个补数相加得7；

④ 7的补数是93；

⑤ 两个补数3和4相乘得12；

⑥ 把步骤④和⑤的得数连在一起就是答案：9312。

请看上图，这个印度速算法是不是很快啊！

我们来探究一下这个方法背后的算术原理。

97×96

=（100－3）（100－4）

=100×100－3×100－4×100+（－3）×（－4）

=10000－700+12

=9312

用代数方法就是

(a+b)(c+d)

=ac+ad+bc+bd

这个方法有个难点就是涉及到负数的运算。上例的b和d就是负数，即－3和－4，两个负数相乘的结果是负负得正，即（－3）×（－4）=12

明白了原理，就可以放心大胆地使用这个神奇的印度速算法了。

计算两位数相乘的方法，除了学校教的竖式计算以外，还有一种交叉相乘法值得推荐，适合心算。

这种算法历史相当悠久，可以追溯到古希腊和古印度的时代，在当时被誉为“闪电算法”或“十字相乘法”。

请看下图：

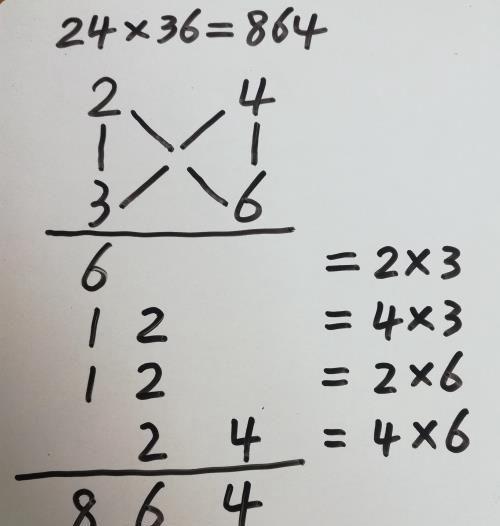
这种简便算法只需稍加练习就能轻松掌握。

修改一下题目：96×96的计算就更加简单了。请看下图。

平方数计算法举例：

96×96

=96²

=（96－4）×100+4×4

=9216

第二章 速算法背后的恒等式

第一章介绍了两个比100略小的数相乘的速算法，速算能够成功，那是因为它建立在恒等式的基础上。让我们把速算背后的恒等式找出来。

这两个比100略小的数，可以用100－a和100－b来表示，可得

（100－a）(100－b)=100(100－a－b)+ab

举一反三，我们根据上面的恒等式稍加变化还能得到两个比100略大的数相乘的速算法。

(100+a)(100+b)=100(100+a+b)+ab

例题请看下图：

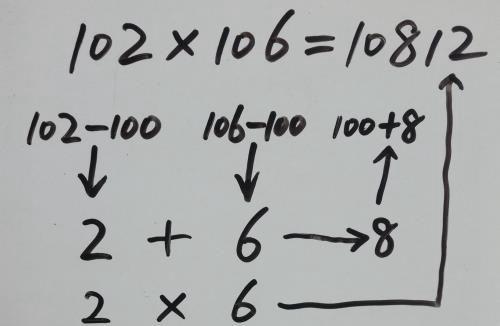
现在我们知道了两个速算法：①两个比100略小的数相乘；②两个比100略大的数相乘。那么，这两个速算法能不能合并成一个呢？大道至简，大家都喜欢简单的东西，当然可以合并，只要引进负数的概念就行了。

举例来说，96的补数是4，102的补数是负数，是－2。减去一个数的补数，如果补数是负数，那么就是加上一个正数；两个补数相乘，如果都是负数，那么负负得正，得数是一个正数。

有了补数可正可负的概念，我们就又前进了一大步，还可以用速算法计算两个这样的数相乘，一个比100略大，另一个比100略小。

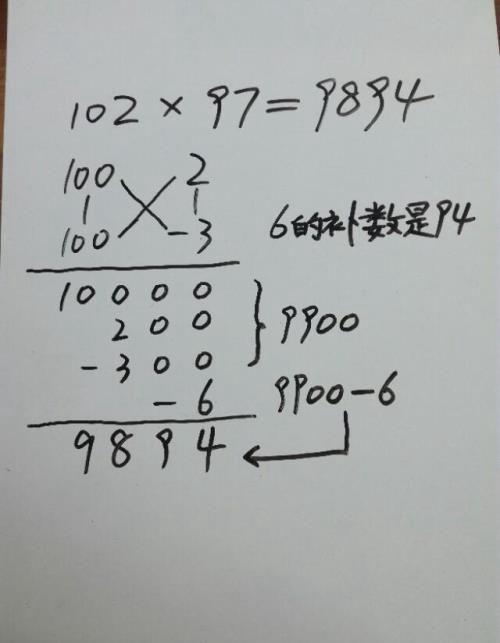
计算步骤：

102-3=99（3是97的补数）；

3×（-2）=-6；

9900-6=9894（减6等于减100+补数94）。

第三章 数形结合速算法

每个恒等式后面都隐藏着一种速算法。再举一个例子。

上图黑子和白子全体组成的正方形边长是a，白子组成的正方形边长是b，那么黑子组成的磬折形面积是多少呢？

如果觉得磬折形面积不好算，那就变成这样的长方形就好啦。请看下图：

这个长方形的长是a+b，宽是a-b。计算这个长方形面积时，我们得到了平方差公式：

a² - b²=（a+b）（a-b）

我们又得到了一种速算法。

举个例子：57×63=3591

57×63

=（60+3）（60-3）

=60² - 3²

=3600-9

=3591

相邻自然数的平方差有什么速算法呢？看下个例子：

18² -17²

=（18+17）（18-17）

=35

再看这种题目能够速算吗？

97×989=95933

用交叉相乘法心算，过程如下：

989×97

=（1000-11）（100-3）

=100000-3000-1100+33

=95933

因为负负得正，所以要加上33。

科学尚未普及，媒体还需努力。感谢阅读，再见。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小萱创作整理编辑！