整体思想在中学数学中的应用(数学整体思想例题及答案)

导语：中考数学中“整体思想”的运用

数学思想是数学知识的进一步提炼和升华，解数学题目除了需要扎实的基础知识外，一定的方法和技巧也不可缺少。尤其是中考题，更需要运用灵活的数学方法和数学思想，将问题简化，

整体思想就是将问题整体化，从整体结构上考虑，明确解题方法，不需一一拆分找出问题的每一个小步骤。我们就通过题目来体会一下：

1、利用两块长方体木块测量一张桌子的高度，首先按图A所示放置，再交换木块位置，按图B所示放置，测量数据如图所示，求桌子的高度。

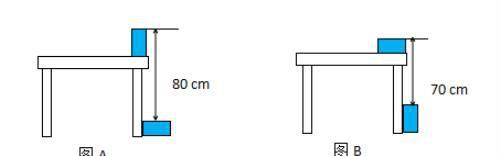
题图

【解析】不用具体地去想办法解出木块的长宽，可以把其看作整体来做。

设木块的长和宽分别为a、b，桌子高度为x。

则有：a+x-b=80，

b+x-a=70，

得：2x=150，x=75. 即桌子高度为75cm。

再如：2、设m、n是一元二次方程 x^2 +3x -7=0的两个根，则m^2 +4m+n=?

【解析】∵ m、n是方程的两个根，

∴ m+n= -3，m^2 +3m -7=0,

∴ m^2 +4m+n=4.

这道题目也是用的整体思想，而不是分别去求m和n的值，求得话当然也可以，但会增加计算量和题目的难度，你觉得呢？

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小冰创作整理编辑！