数量关系容斥问题公式(数量关系中容斥原理公式)

导语：数量关系——容斥问题

一、两集容斥

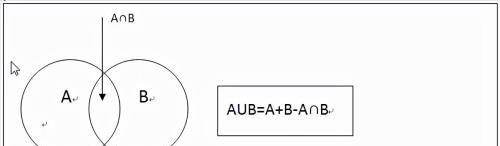
两集容斥原理图

二、三集容斥（☆重点掌握☆）

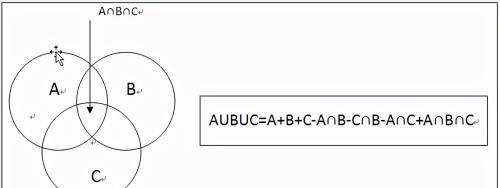
三集容斥原理图

三集容斥考察率比较高，题目也比较典型，这是掌握重点。需要重点理解原理、记忆公式。

【例题】某单位共有240名员工，其中订阅A期刊的有125人，订阅B期刊的有126人，订阅C期刊的有135人，订阅A、B期刊的有57人，订阅A、C期刊的有73人，订阅3种期刊的有31人，此外，还有17人没有订阅这三种期刊中的任何一种。问订阅B、C期刊的有多少人?

A.57

B.64

C.69

D.78

方法一：公式法。本题考查容斥原理中三集合容斥，按照给出的数据可采用公式法解题。设订阅B、C期刊的有x人，根据三集容斥公式可列方程：125+126+135-57-73-x+31=240-17，解得x=64。因此，选择B选项。

方法二：填充法。如下图所示，设订阅B、C期刊的有x人，然后将已知填充。最后将全集加起来则有：

26+42+93-x+x-31+100-x+26+31=240-17；最后可求出x=64。

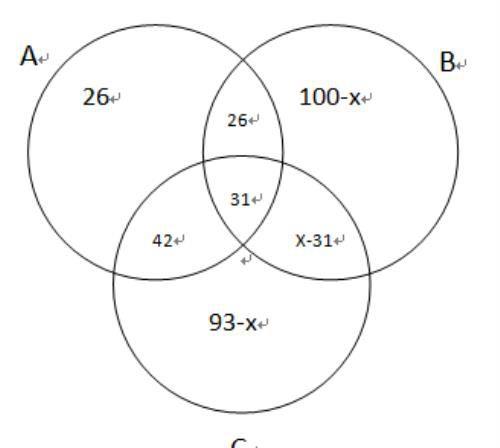
填充法

解题方法：1、公式法。2、画图填充法。（将原理图画出来，首先填充最中间数字，再依次向外填充，相关数字填充进去，而后求解未知项）

三、容斥极值

I表示全集

A∩B最小值=A+B-I；

A∩B∩C最小值=A+B+C-2I；

A∩B∩C∩D最小值=A+B+C+D-3I；

以此类推。

【例题】某社团共有46人，其中35人爱好戏剧，30人爱好体育，38人爱好写作，40人爱好收藏。问这个社团至少有多少人以上四项活动都喜欢？

A.5

B.6

C.7

D.8

解析：根据容斥极值问题公式：A∩B∩C∩D最小值=A+B+C+D-3I；可以得到以上四项活动都喜欢至少有35+30+38+40-3×46=5人。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小面创作整理编辑！