动点问题几何难还是函数难学(几何动点问题中的函数图像)

导语：动点问题，几何难，还是函数难？

说到动点问题，相信大家都不会陌生，因其具有难度较大、综合性较强、解法灵活等鲜明特点，加上在解题过程中，需要学生熟练运用数形结合、分类讨论等数学思想方法，这些都提升了动点问题的学习难度。因此，与动点有关的问题一直是全国各地中考数学热门考查对象。

从“发现问题→分析问题→解决问题”的角度来讲，再难的问题，我们都可以分割成若干个基本问题进行分类解决，就像在众多中考数学动点问题当中，最常见的就是几何有关的动点问题和函数有关的动点问题。

在初中数学学习过程中，动点问题并不是以某一章节整块知识内容的形式出现，而是将整个初中阶段所学的数学知识进行升级和综合。大部分情况下，动点问题都是以运动的点、线段、变化的角、图形的面积为基本条件，给出一个或多个变量，要求确定变量与其他量之间的函数等其他关系；或变量在一定条件为定值时，进行相关的计算和综合解答，解答这类题目，一般要根据点的运动和图形的变化过程，对其不同情况进行分类求解。

如几何有关的动点问题，主要是以几何知识和具体的几何图形为背景，在几何图形中渗透运动变化的观点，通过点、线、形的运动，图形的平移、翻折、旋转等等把图形的有关性质和图形之间的数量关系和位置关系看作是在变化的、相互依存的状态之中。

动点有关的综合问题，典型例题分析1：

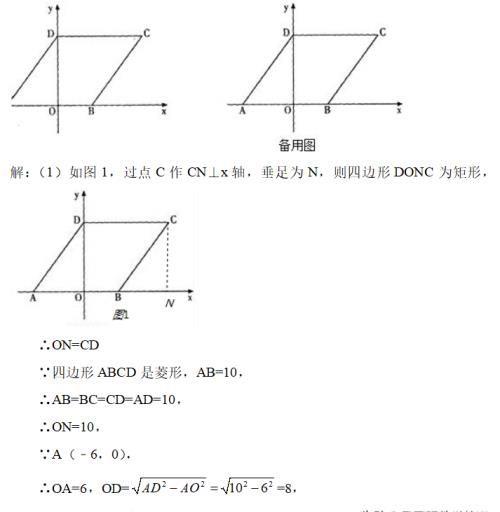
在平面直角坐标系中，点0是坐标原点，四边形ABCD为菱形，AB边在x轴上，点D在y轴上，点A的坐标是（﹣6，0），AB=10．

（1）求点C的坐标：

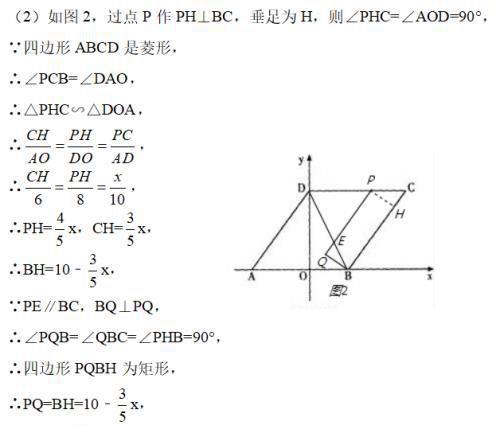
（2）连接BD，点P是线段CD上一动点（点P不与C、D两点重合），过点P作PE∥BC交BD与点E，过点B作BQ⊥PE交PE的延长线于点Q．设PC的长为x，PQ的长为y，求y与x之间的函数关系式（直接写出自变量x的取值范围）；

（3）在（2）的条件下，连接AQ、AE，当x为何值时，S△BOE+S△AQE=4S△DEP/5并判断此时以点P为圆心，以5为半径的⊙P与直线BC的位置关系，请说明理由．

考点分析：

相似三角形的判定与性质；勾股定理；菱形的性质；矩形的判定与性质；直线与圆的位置关系；代数几何综合题。

题干分析：

（1）过点C作CN⊥x轴，垂足为N，求得CN、ON的长，即可得出坐标；

（2）过点P作PH⊥BC，垂足为H，易证△PHC∽△DOA，可得CH=3x/5，BH=10﹣3x/5；然后证明四边形PQBH为矩形，则PQ=BH，即可求得；

（3）过点P作PH′⊥BC，垂足为H′，过点D作DG⊥PQ于点G，过点A作AF⊥PQ交PQ的延长线于点F，用x分别表示出EQ、BQ、AF的值和PE、DG的值，然后，根据S△BOE+S△AQE=4S△DEP/5，可求出x的值，最后根据PH′的值与x的值比较，即可得出其位置关系；

解题反思：

本题考查了菱形、矩形的判定及性质、相似三角形的判定及性质、勾股定理的运用及直线与圆的位置关系，本题考查知识较多，属综合性题目，考查了学生对知识的掌握程度及熟练运用所学知识解答题目的能力．

俗话说“点动成线，线动成面”，所以动点问题基本上都会牵扯到几何知识，你要吃透动点综合问题，就需要吃透几何知识。

要想学好初中数学，函数永远是绕不开的话题，就像动点问题一样。与函数有关的动点问题，难度在于它综合了初中阶段所学的一次函数、反比例函数、二次函数的图像和性质，以及相关的三角形、四边形（包含特殊平行四边形）、圆等几何图形，将初中阶段所学的知识综合在一起，考查了学生知识综合运用能力和解决复杂问题的能力。

动点有关的综合问题，典型例题分析2：

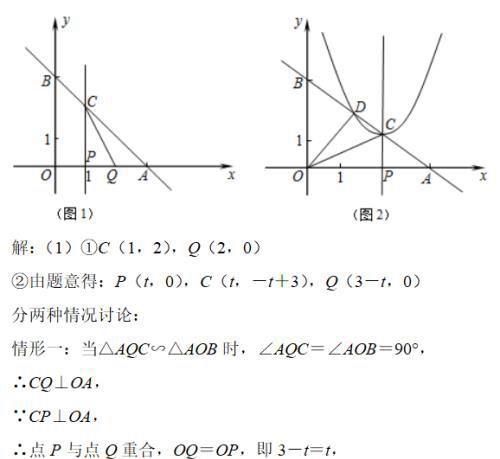
已知直线y＝kx＋3（k＜0）分别交x轴、y轴于A、B两点，线段OA上有一动点P由原点O向点A运动，速度为每秒1个单位长度，过点P作x轴的垂线交直线AB于点C，设运动时间为t秒．

（1）当k＝－1时，线段OA上另有一动点Q由点A向点O运动，它与点P以相同速度同时出发，当点P到达点A时两点同时停止运动（如图1）．

①直接写出t＝1秒时C、Q两点的坐标；

②若以Q、C、A为顶点的三角形与△AOB相似，求t的值．

（2）当k＝-3/4时，设以C为顶点的抛物线y＝（x＋m）2＋n与直线AB的另一交点为D（如图2），

①求CD的长；

②设△COD的OC边上的高为h，当t为何值时，h的值最大？

考点分析：

二次函数综合题、几何代数综合题。

题干分析：

（1）①由题意得．②由题意得到关于t的坐标．按照两种情形解答，从而得到答案．（2）①以点C为顶点的抛物线，解得关于t的根，又由过点D作DE⊥CP于点E，则∠DEC＝∠AOB＝90°，又由△DEC∽△AOB从而解得．②先求得三角形COD的面积为定值，又由Rt△PCO∽Rt△OAB，在线段比例中t为36/25是，h最大．

解题反思：

本题考查了二次函数的综合题，（1）①由题意很容易知，由题意知P（t，0），C（t，－t＋3），Q（3－t，0）代入，分两种情况解答．（2）①以点C为顶点的函数式，设法代入关于t的方程，又由△DEC∽△AOB从而解得．②通过求解可知三角形COD的面积为定值，又由Rt△PCO∽Rt△OAB，在线段比例中t为36/25是，h最大．从而解答．

面对动点问题，大多数学生解题时都会感到手无足措，主要是没有具体的知识定理来解决此问题，具体变现在以下：

找不准变量与不变量之间的关系；

不能准确的理解点或线的运动过程；

对于不相关的两个量的函数关系式的求得感到困难；

有的学生无法准确读懂题的意思；

面对分类讨论问题的时候，出现考虑的情况不全面；

结果的取舍不知道怎么处理等。

因此，基于这样的实际学习情况，每位学生要做的就是除了掌握好几本的知识定理和方法技巧，更要努力提高解决问题和分析问题的能力，熟练运用各种数学思想方法，如常见的方程思想、数学建模思想、函数思想、转化思想、分类讨论法、数形结合法等。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小玥创作整理编辑！